Нотация “большое О”¶
При попытке охарактеризовать эффективность алгоритма в терминах времени выполнения независимо от конкретной программы или компьютера, очень важно оценить количество операций или шагов, которые ему потребуются. Если каждый из этих шагов принять за базовую единицу вычисления, то время выполнения алгоритма может быть выражено, как количество операций, требуемых для решения задачи. Принятие решение о том, что же является таким базовым блоком вычисления, может стать сложной задачей, зависящей от того, как алгоритм реализован.
Хорошей базовой единицей вычисления для сравнения суммирующих алгоритмов, показанных ранее, может служить количество операций присваивания, используемых при подсчёте суммы. В функции sumOfN есть только таких присваиваний 1 (\(theSum = 0\)) плюс n (сколько раз мы вычисляем \(theSum=theSum+i\)). Эту величину можно обозначить \(T\), где \(T(n)=1 + n\). Параметр \(n\) часто называют “размером задания”, так что мы можем прочитать формулу как “\(T(n)\) - это время, необходимое для решения задачи, размером \(n\), за \(1+n\) шагов.”
В представленных выше функциях суммирования для обозначения размера задачи имеет смысл использовать количество слагаемых. Так мы сможем сказать, что суммирование первых 100 000 целых - задание большее, чем суммирование первой тысячи. Поэтому выглядит разумным положение, что время, требуемое на решение большего случая, будет больше, чем для меньшего случая. Таким образом, наша цель - показать, как время работы алгоритма изменяется в зависимости от размера задачи.
Учёные-информатики при использовании такой техники анализа предпочитают идти на один шаг дальше. Выходит так, что точное количество операций не так важно, как определение доминирующей части функции \(T(n)\). Другими словами, когда задание становится больше, некая часть функции \(T(n)\), как правило, перекрывает всё остальное. Эта доминирующая часть в итоге и используется при сравнении. Функция порядка величины описывает ту часть \(T(n)\), которая сильнее возрастает при росте \(n\). Порядок величины часто называют нотацией “большое О” (от англ order - “порядок”) и записывают как \(O(f(n))\). Она предоставляет собой целесообразное приближение к действительному числу шагов в вычислении. Функция \(f(n)\) является простым представлением доминирующей части оригинальной \(T(n)\).
В примере выше \(T(n)=1+n\). Чем больше становится \(n\), тем менее значима для конечного результата константа 1. При поиске приближения для \(T(n)\) мы можем отбросить 1 и просто сказать, что временем выполнения является \(O(n)\). Важно отметить, что 1 безусловно важна для \(T(n)\). Однако, при росте \(n\) наше приближение и без неё останется столь же точным.
Ещё один пример: предположим, что для некоего алгоритма точное число шагов \(T(n)=5n^{2}+27n+1005\). При малых \(n\) (скажем, 1 или 2) константа 1005 выглядит доминирующей частью функции. Однако, с ростом \(n\) превалирующим становится слагаемое \(n^{2}\). Фактически, когда \(n\) действительно велико, то два других слагаемых перестают играть хоть какую-нибудь значимую роль в определении конечного результата. Ещё раз, аппроксимируя \(T(n)\) с ростом \(n\), мы можем игнорировать другие слагаемые и сфокусироваться только на \(5n^{2}\). Дополнительно, коэффициент \(5\) тоже становится неважным при увеличении \(n\). Так что можно сказать, что функция \(T(n)\) имеет порядок величины \(f(n)=n^{2}\), или просто \(O(n^{2})\).
Хотя мы и не видим этого в примере с суммированием, иногда производительность алгоритма зависит от точных значений данных больше, чем от размера задачи. Для алгоритмов такого рода нужно характеризовать их эффективность с точки зрения наилучшего, наихудшего или усреднённого случая. Производительность для худшего случая относится к определённому набору данных, на котором алгоритм выполняется особенно плохо. В то время как различные наборы данных для точно такого же алгоритма могут иметь необычайно хорошую производительность, в большинстве случаев алгоритм имеет производительность где-то по середине между этими двумя экстремумами (усреднённый случай). Учёным-информатикам важно понимать эти различия, чтобы не впасть в заблуждение при рассмотрении одного конкретного случая.
Некоторые функции порядка величины очень распространены и в процессе изучения алгоритмов будут попадаться вам вновь и вновь. Все они представлены в таблице 1. Для того, чтобы увидеть, какая из них является доминирующей частью любой функции \(T(n)\), мы должны видеть, как они соотносятся друг с другом при возрастании \(n\).
| f(n) | Название |
|---|---|
| \(1\) | Константная |
| \(\log n\) | Логарифмическая |
| \(n\) | Линейная |
| \(n\log n\) | Линейно-логарифмическая |
| \(n^{2}\) | Квадратичная |
| \(n^{3}\) | Кубическая |
| \(2^{n}\) | Экспоненциальная |
На рисунке 1 показаны графики функций из таблицы 1. Обратите внимание, что при малых \(n\) их нелегко отличить друг от друга и тяжело сказать, кто же из них доминирует. Однако, как только \(n\) вырастает, появляется определённая зависимость, и легко увидеть, как функции соотносятся друг с другом.
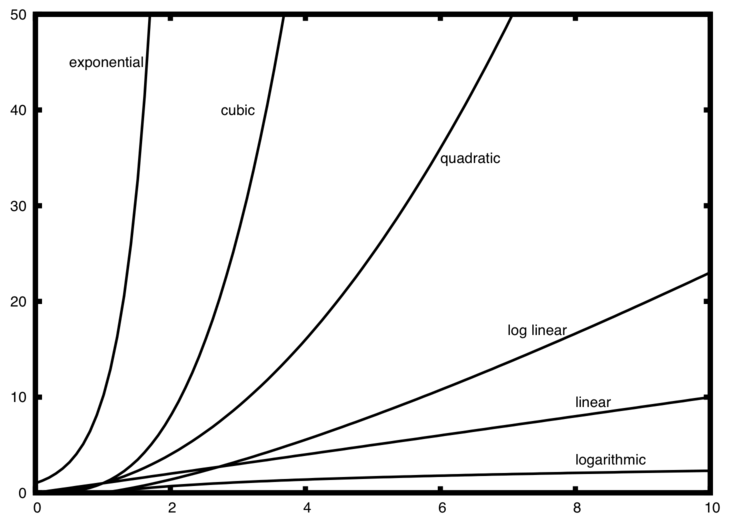
Рисунок 1: Графики распространённых функций “большое О”
В качестве заключительного примера предположим, что у нас есть фрагмент кода на Python, показанный в листинге 2. Несмотря на то, что на самом деле эта программа ничего не делает, полезно будет посмотреть, как мы можем взять существующий код и проанализировать его производительность.
Листинг 2
a=5
b=6
c=10
for i in range(n):
for j in range(n):
x = i * i
y = j * j
z = i * j
for k in range(n):
w = a*k + 45
v = b*b
d = 33
Число операций присваивания представляет собой сумму из четырёх слагаемых. Первое - константа 3, отражающая три присваивания в начале фрагмента. Второе - \(3n^{2}\), поскольку три присваивания выполняются \(n^{2}\) раз внутри вложенной итерации. Третье - \(2n\) - два присваивания, повторяющиеся \(n\) раз. Наконец, четвёртое слагаемое - константа 1, представляющая последний оператор присваивания. Всё вместе это даёт \(T(n)=3+3n^{2}+2n+1=3n^{2}+2n+4\). Глядя на степени, мы легко можем заметить, что слагаемое \(n^{2}\) будет доминантой, и следовательно, этот фрагмент кода является \(O(n^{2})\). Обратите внимание, что прочие слагаемые (так же, как и коэффициенты) при возрастании \(n\) можно проигнорировать.
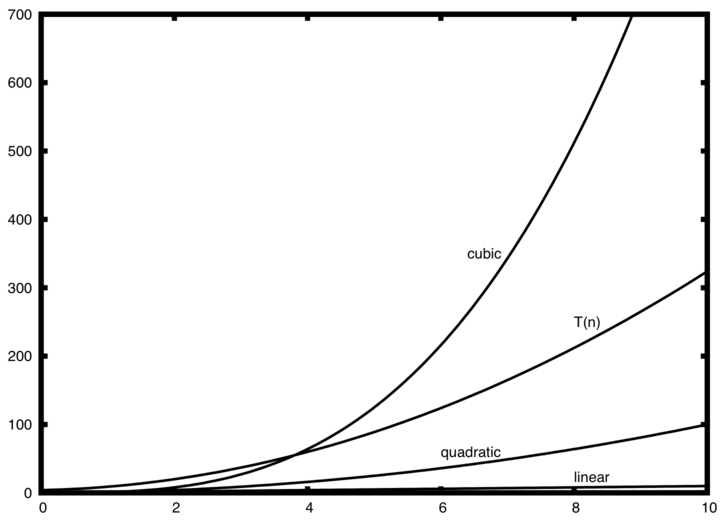
Рисунок 2: Сравнение \(T(n)\) с распространёнными функциями “большого О”
На рисунке 2 показаны графики нескольких распространённых функций “большое О” в сравнении с обсуждаемой выше функцией \(T(n)\). Обратите внимание, что в изначально \(T(n)\) больше, чем кубическая функция, но с ростом \(n\) последняя быстро берёт верх над \(T(n)\) Так же легко увидеть, что с ростом \(n\) \(T(n)\) следует квадратичной функции.
Самопроверка
Напишите на Python две функции для поиска минимального значения в списке. Первая из них должна сравнивать каждое число со всеми другими значениями в списке. \(O(n^2)\). Вторая функция должна быть линейной с \(O(n)\)