Списки¶
Разработчики Python имели широкий выбор, когда реализовывали списки как структуру данных. Каждое их решение оказывает влияние на скорость выполнения операций со списками. Чтобы принять верное решение, они смотрели на то, для чего пользователи используют списки чаще всего, и оптимизировали реализацию таким образом, чтобы наиболее распространённые операции совершались очень быстро. Конечно, разработчики так же старались сделать быстрыми и менее используемые операции, но при поиске компромиссов производительность последних приносилась в жертву более распространённым.
Двумя наиболее частыми операциями над списками являются индексация и присваивание на заданную позицию. Обе они занимают равное количество времени, вне зависимости от того, насколько велик список. Когда операции не зависят от размера списка (как названные выше), говорят, что они имеют \(O(1)\)
Другим часто встречающимся программистским заданием является увеличение списка. Существует два способа продлить список. Вы можете использовать метод добавления или оператор конкатенации. Первый является \(O(1)\), но вот второй имеет \(O(k)\), где \(k\) - размер списка, который будет присоединён. Польза от этой информации в том, что она помогает сделать ваши программы более эффективными, выбирая правильный инструмент для работы.
Давайте рассмотрим четыре разных способа сгенерировать список из n чисел, начинающийся с нуля. Сначала мы попробуем цикл for и создадим список с помощью конкатенации. Затем используем для этого метод append. Далее попытаемся создать список, используя генераторы списков. И, наконец, используем для этого, возможно, самый очевидный способ - функцию range, обёрнутую в конструктор списка. Листинг 3 показывает код для всех этих четырёх способов.
Листинг 3
def test1():
l = []
for i in range(1000):
l = l + [i]
def test2():
l = []
for i in range(1000):
l.append(i)
def test3():
l = [i for i in range(1000)]
def test4():
l = list(range(1000))
Чтобы получить время, требуемое для выполнения каждой функции, мы используем модуль Python timeit. Он разработан для того, чтобы разработчики могли делать кроссплатформенные синхронные измерения, запуская функции в согласованной среде и используя механизмы синхронизации, максимально схожие между собой для разных операционных систем.
Чтобы использовать timeit, вам нужно создать объект Timer, чьими параметрами являются два оператора Python. Первый из них сообщает, что вам нужно время; второй - что тест будет проводиться один раз. Модуль timeit замерит время, необходимое для выполнения операции, несколько раз. По умолчанию он попытается запустить операцию один миллион раз. Когда это будет сделано, время вернётся, как число с плавающей запятой, представляющее собой общее количество секунд. Однако, поскольку оператор вычислялся миллион раз, то вы можете прочитать результат, как количество микросекунд, затраченных на выполнение одного теста. Так же в timeit можно передать именованный параметр number, который позволит вам конкретизировать, сколько раз нужно запустить оператор. Следующий фрагмент показывает, как долго занимает запуск каждой тестовой функции тысячу раз.
t1 = Timer("test1()", "from __main__ import test1")
print("concat ",t1.timeit(number=1000), "milliseconds")
t2 = Timer("test2()", "from __main__ import test2")
print("append ",t2.timeit(number=1000), "milliseconds")
t3 = Timer("test3()", "from __main__ import test3")
print("comprehension ",t3.timeit(number=1000), "milliseconds")
t4 = Timer("test4()", "from __main__ import test4")
print("list range ",t4.timeit(number=1000), "milliseconds")
concat 6.54352807999 milliseconds
append 0.306292057037 milliseconds
comprehension 0.147661924362 milliseconds
list range 0.0655000209808 milliseconds
В эксперименте выше мы замеряли время для функций test1(), test2() и так далее. Оператор начальной установки может показать вам очень необычным, так что давайте разберём детали. Возможно, вы хорошо знакомы с операторами from и import`, но они обычно используются в начале файлов программ на Python. В этом случае, оператор from __main__ import test1 импортирует функцию test1 из пространства имён __main__ в пространство имён, где ставит свой временн*о*й эксперимент timeit. Это делается, чтобы запускать тесты в среде с отсутствующими бродячими переменными, которые вы могли ненароком создать и которые могут повлиять на производительность функции непредвиденным образом.
Из эксперимента выше совершенно ясно, что операция append с 0.30 миллисекундами быстрее, чем конкатенация с её 6.54 миллисекундами. Также мы видим время, требуемое для двух дополнительных методов создания списков: использования конструктора списка с вызовом range и генератора списков. Интересно, что последний в два раза быстрее, чем цикл for с операцией append.
Наше последнее наблюдение в этом маленьком эксперименте заключается в том, что все времена, которые вы видите выше, содержат некоторые издержки при фактическом вызове тестовой функции. Однако, мы можем предположить, что для всех четырёх случаев эта величина одинакова, так что мы по-прежнему имеем адекватное сравнение операций. Поэтому правильно говорить не “конкатенация занимает 6.54 миллисекунд”, а “тестовая функция конкатенации выполняется 6.54 миллисекунд”. В качестве упражнения, вы можете провести временн*о*й тест для пустой функции и вычесть его результат из чисел выше.
После того, как мы увидели, как конкретно может быть измерена производительность, вы можете посмотреть в таблицу 2, чтобы узнать эффективность в терминах “большого О” для основных операций над списками. После вдумчивого размышления над ней, вы можете заинтересоваться двумя разными временами для pop. Когда этот метод вызывается для конца списка, это занимает \(O(1)\). Но когда pop вызывают для первого или любого другого элемента из середины списка, он имеет \(O(n)\). Причина кроется в том, как в Python выбрана реализация списков. Когда элемент берётся из начала списка, то все прочие элементы смещаются на одну позицию вперёд. Сейчас это может показаться вам глупым, но если вы посмотрите на таблицу 2, то увидите, что эта же реализация позволяет операции индексации иметь \(O(1)\). Это один из тех компромиссов, которые разработчики Python сочли разумными.
| Операция | Эффективность |
|---|---|
| index [] | O(1) |
| Присваивание по индексу | O(1) |
| append | O(1) |
| pop() | O(1) |
| pop(i) | O(n) |
| insert(i,item) | O(n) |
| оператор del | O(n) |
| итерирование | O(n) |
| вхождение (in) | O(n) |
| срез [x:y] | O(k) |
| удалить срез | O(n) |
| задать срез | O(n+k) |
| обратить | O(n) |
| конкантенация | O(k) |
| сортировка | O(n log n) |
| размножить | O(nk) |
В качестве способа демонстрации этих различий в производительности, давайте проведём другой эксперимент с использованием модуля timeit. Нашей целью будет возможность проверки производительности операции pop на списке известного размера, когда программа выталкивает элемент из конца списка, и ещё раз - когда программа вталкивает элемент из начала списка. Мы также произведём замеры времени на списках разной длины. Что мы ожидаем увидеть, так это то, что временн*а*я зависимость у выталкивания из конца списка остаётся одинаковой при увеличении списка, в то время как выталкивание из начала списка будет расти вместе с его длиной.
Листинг 10 демонстрирует попытку замерить разницу между двумя использованиями pop. Как видно из первого примера, выталкивание с конца занимает 0.0003 миллисекунды, в то время как на выталкивание из начала требуется 4.82 миллисекунды. Для списка в два миллиона элементов коэффициент будет 16 000.
Есть ещё несколько замечаний относительно листинга 4. Первое - это оператор from __main__ import x. Несмотря на то, что мы не определяли функцию, мы хотим иметь возможность использовать список-объект x в нашем тесте. Этот подход позволяет нам замерять время только для единственной pop-операции и получать для неё наиболее точное значение. Поскольку замеры повторяются тысячу раз, то также важно отметить, что список уменьшается в размерах на единицу за каждую итерацию. Но поскольку изначально в нём два миллиона элементов, то общий объём уменьшится примерно на \(0.05\%\)
Листинг 4
popzero = timeit.Timer("x.pop(0)",
"from __main__ import x")
popend = timeit.Timer("x.pop()",
"from __main__ import x")
x = list(range(2000000))
popzero.timeit(number=1000)
4.8213560581207275
x = list(range(2000000))
popend.timeit(number=1000)
0.0003161430358886719
Пока наш первый тест показывает, что pop(0) действительно медленнее pop(). Но он не подтверждает заявление, что pop(0) является \(O(n)\), в то время как pop() - \(O(1)\). Чтобы доказать это, нам нужно рассмотреть производительность обоих вызовов на диапазоне размеров списков. Листинг 5 содержит этот тест.
Листинг 5
popzero = Timer("x.pop(0)",
"from __main__ import x")
popend = Timer("x.pop()",
"from __main__ import x")
print("pop(0) pop()")
for i in range(1000000,100000001,1000000):
x = list(range(i))
pt = popend.timeit(number=1000)
x = list(range(i))
pz = popzero.timeit(number=1000)
print("%15.5f, %15.5f" %(pz,pt))
На рисунке 3 показаны результаты нашего эксперимента. Вы можете видеть, как список становится всё длиннее и длиннее, а время, необходимое для pop(0) - больше и больше, тогда как график для pop остаётся плоским. Это в точности то, что мы ожидали увидеть от алгоритмов с \(O(n)\) и \(O(1)\)
Некоторым источником ошибок в нашем маленьком эксперименте стал тот факт, что на компьютере запущены и другие процессы, которые могут замедлять код. Несмотря на то, что мы старались минимизировать влияние прочих происходящих в компьютере вещей, с ними связаны некоторые флуктуации времён. Именно поэтому цикл выполняет тест тысячу раз - в первую очередь, чтобы статистически собрать достаточно информации для утверждения о надёжности измерений.
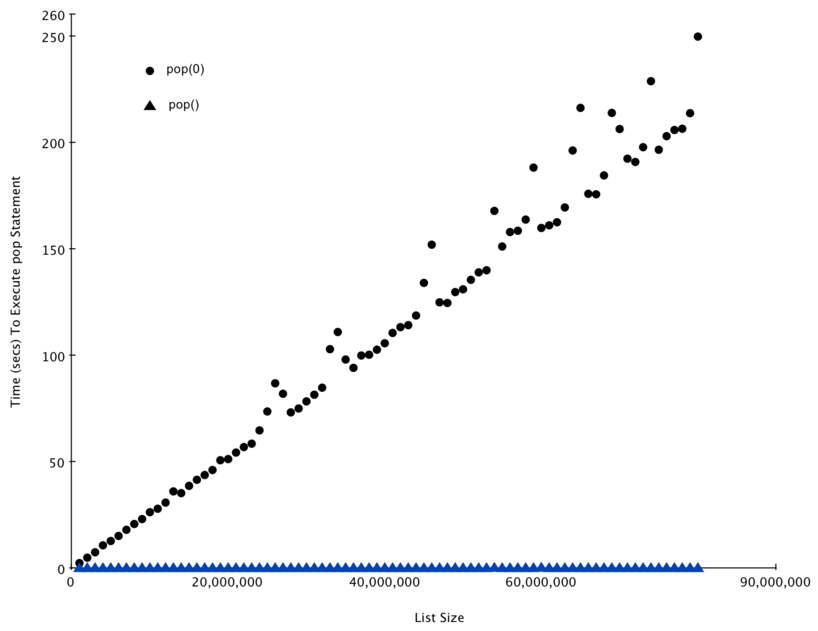
Рисунок 3: Сравнение производительности pop и pop(0)