Реализация неупорядоченного списка: связанные списки¶
Для реализации неупорядоченного списка мы создадим то, что обычно называют связанным списком. Напомним: мы должны быть уверены, что сможем поддерживать порядок взаимного расположения элементов. Однако, такое позиционирование не обязательно должно быть на смежных участках памяти. Рассмотрим для примера коллекцию элементов, показанную на рисунке 1. Похоже, эти значения были размещены случайным образом. Если мы сможем сохранить в каждом элементе некую явную информацию о размещении его соседа (см. рисунок 2), то соответствующая позиция каждого из них может быть выражена простой ссылкой от одного к другому.

Рисунок 1: Элементы не ограничены в своём физическом размещении.
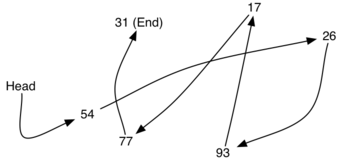
Рисунок 2: Соответствующие позиции определяются с помощью явных ссылок.
Важно отметить, что положение первого элемента должно быть определено явно. Поскольку мы знаем, где он находится, то можем найти местоположение второго и так далее. Внешнюю ссылку часто называют головой списка. Аналогично, последнему элементу нужно знать, что за ним больше ничего нет.
Класс Node¶
Основным строительным блоком в реализации связанного списка является узел. Каждый такой объект должен обладать как минимум двумя информационными составляющими. Во-первых, узел должен содержать сам элемент списка. Мы назовём это полем данных узла. Дополнительно он должен хранить ссылку на следующий узел. Листинг 1 демонстрирует реализацию этой идеи на Python. Чтобы создать узел, вы должны предоставить начальное значение его данных. Вычисление оператора присваивания ниже даст объект “узел”, содержащий значение 93 (см. рисунок 3). Следует отметить, что обычно мы представляем узел-объект, как это показано на рисунке 4. Класс Node также включает обычные методы для доступа и модификации полей данных и ссылки на следующий узел.
Листинг 1
class Node:
def __init__(self,initdata):
self.data = initdata
self.next = None
def getData(self):
return self.data
def getNext(self):
return self.next
def setData(self,newdata):
self.data = newdata
def setNext(self,newnext):
self.next = newnext
Мы создаём объект Node обычным способом.
>>> temp = Node(93)
>>> temp.getData()
93
Специальное ссылочное значение Python None играет важную роль и в классе Node, и в самом связанном списке. Обратите внимание, что конструктор первоначально создаёт узел с next, установленным в None. Явное присвоение None начальному значению ссылки на следующий элемент - неизменно хорошая идея.
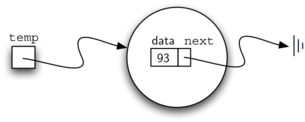
Рисунок 3: Объект Node, содержащий значение и ссылку на следующий узел
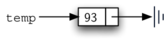
Рисунок 4: Типичное представление узла
Класс Unordered List¶
Как мы предлагали выше, неупорядоченный список будет представлять из себя коллекцию узлов, каждый из которых связан со следующим посредством явной ссылки. Пока мы знаем, как найти первый узел (содержащий первый элемент), каждый последующий будет обнаружен с помощью успешного следования по ссылкам. Имея это ввиду, класс UnorderedList должен содержать ссылку на первый узел. В листинге 2 показан конструктор такого класса. Заметьте, что каждый объект списка будет поддерживать единственную ссылку на свою “голову”.
Листинг 2
class UnorderedList:
def __init__(self):
self.head = None
Первоначально мы создадим пустой список. Оператор присваивания
>>> mylist = UnorderedList()
создаст представление связанного списка, показанного на рисунке 5. Как мы уже обсуждали для класса Node, специальная ссылка None вновь будет использоваться в качестве состояния, когда голова списка ни на что не ссылается. В конечном счёте, список из данного ранее примера будет представлен в виде связанного списка, как это показано на рисунке 6. Голова списка ссылается на первый узел, содержащий первый элемент списка. В свою очередь, этот узел содержит ссылку на следующий узел (следующий элемент) и так далее. Очень важно отметить, что класс списка сам по себе не содержит каких-либо объектов-узлов. Он имеет только единственную ссылку на первый узел связанной структуры.
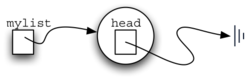
Рисунок 5: Пустой список
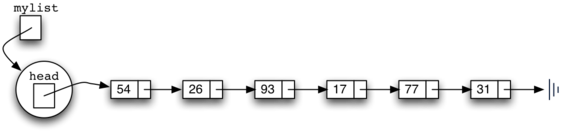
Рисунок 6: Связанный список целых чисел
Метод isEmpty, показанный в листинге 3, просто проверяет, ссылается ли голова списка на None. Результат булева выражения self.head==None будет истинным только если в связанном списке нет узлов. Поскольку новый список пуст, то конструктор и проверка на пустоту должны согласовываться друг с другом. Это демонстрирует преимущества использования ссылки None для определения “конца” связанной структуры. В Python None можно сравнивать с любой ссылкой. Две ссылки равны, если они обе ссылаются на один объект. В оставшихся методах мы будем часто использовать этот факт.
Листинг 3
def isEmpty(self):
return self.head == None
Итак, как же нам поместить элементы в наш список? Для этого нужно реализовать метод add. Однако, перед этим стоит ответить на важный вопрос: где в связанном списке размещать новый элемент? Поскольку, он неупорядочен, то в конкретизации местоположения нового элемента по отношению к уже существующим нет необходимости. Т.е. вставку можно осуществить в любом месте. Принимая это во внимание, имеет смысл поместить новое значение в самую легкодоступную позицию.
Напомним, что структура связанного списка предоставляет нам всего одну точку входа - голову списка. Все прочие узлы можно достигнуть только через доступ к первому узлу по цепочке из ссылок next. Это подразумевает, что самое простое место для добавления нового узла - это голова, начало списка. Другими словами, мы будем создавать новый элемент в качестве первого в списке, а существующие элементы нужно будет связать так, чтобы они следовали за ним.
Связанный список, показанный на рисунке 6, был построен с помощь вызова метода add несколько раз.
>>> mylist.add(31)
>>> mylist.add(77)
>>> mylist.add(17)
>>> mylist.add(93)
>>> mylist.add(26)
>>> mylist.add(54)
Обратите внимание: поскольку 31 - первый из добавленных в список элементов, то он же, в конечном итоге, и последний узел связанного списка, так как все прочие элементы добавляются перед ним. Аналогично, 54 - последний добавленный элемент, и он будет значением первого узла связанного списка.
Метод add показан в листинге 4. Каждый элемент должен быто обёрнут в объект Node. Строка 2 создаёт новый узел и размещает в его поле данных заданный элемент. Теперь нужно завершить процесс, связав новый узел с существующей структурой. Это требует двух шагов, показанных на рисунке 7. Шаг 1 (строка 3) изменяет ссылку next нового узла, чтобы она указывала на предыдущий. Теперь, когда остаток соответствующим образом присоединён к новому узлу, мы можем изменить голову списка, чтобы она тоже ссылалась на новый узел. Этим занимается оператор присваивания в строке 4.
Порядок двух описанных выше шагов очень важен. Что произойдёт, если поменять местами строки 3 и 4? Если первым произойдёт изменение головы списка, то результат можно увидеть на рисунке 8. Поскольку голова - единственная внешняя ссылка на список узлов, то все изначальные данные будут потеряны и получить к ним доступ больше не удастся.
Листинг 4
def add(self,item):
temp = Node(item)
temp.setNext(self.head)
self.head = temp
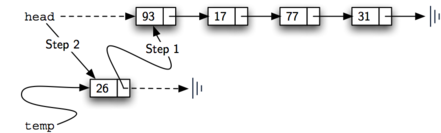
Рисунок 7: Добавление нового узла в два шага
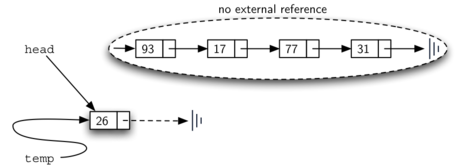
Рисунок 8: Результат обратного порядка двух шагов
Следующими методами, который мы реализуем, будут size, search и remove. Все они основаны на технике обхода связанного списка. Она подразумевает процесс поочерёдного посещения каждого узла. Чтобы сделать это, используем внешнюю ссылку в качестве стартовой. Поскольку мы посещаем каждый узел, то она будет перемещаться по next-ам элементов списка.
Для реализации метода size достаточно просто обойти связанный список и подсчитать количество встреченных узлов. Листинг 5 демонстрирует код на Python, выполняющий эту работу. Внешняя ссылка называется current и инициализируется головой списка в строке 2. В начале обработки мы не видим каких-либо узлов, поэтому счёт равен нулю. Строки 4-6 реализуют собственно обход. До тех пор, пока текущая ссылка не похожа на конец списка (None), мы перемещаем её на следующий узел с помощью оператора присваивания в строке 6. Отметим ещё раз, что возможность сравнивать ссылки с None очень полезна. Каждый раз перемещаясь на новый узел, мы прибавляем к count единицу. После окончания итераций count возвращается в качестве результата. Рисунок 9 показывает, как происходит обработка по мере продвижения вниз по списку.
Листинг 5
1 2 3 4 5 6 7 8 | def size(self):
current = self.head
count = 0
while current != None:
count = count + 1
current = current.getNext()
return count
|
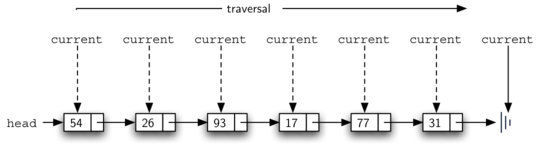
Рисунок 9: Обход связанного списка от головы до конца
Реализация поиска значения в связанном списке для неупорядоченного списка также использует технику обхода. В процессе посещения каждого узла мы запрашиваем, как его данные соотносятся с тем элементом, который мы ищем. Однако, в этом случае нам может и не понадобиться обходить весь список до конца. Фактически, если мы добрались до конца списка, то искомого элемента он не содержит. А если мы нашли нужное, то нет смысла продолжать обход.
Листинг 6 показывает реализацию метода search. Как и в методе size обход начинается с головы списка (строка 2). Мы также используем булеву переменную found, чтобы помнить, нашли ли мы искомое. Поскольку в начале обхода ещё ничего не найдено, то found устанавливается в False (строка 3). Цикл в строке 4 принимает оба описанных выше условия. До тех пор, пока есть узлы для посещения и искомый элемент не найден, мы продолжаем проверку. Строка 5 спрашивает: не находится ли в этом узле то, что нам нужно? Если ответ “да”, то found выставляется в True.
Листинг 6
1 2 3 4 5 6 7 8 9 10 | def search(self,item):
current = self.head
found = False
while current != None and not found:
if current.getData() == item:
found = True
else:
current = current.getNext()
return found
|
В качестве примера рассмотрим вызов метода search для поиска элемента 17.
>>> mylist.search(17)
True
Поскольку 17 в списке присутствует, то обход будет происходить до тех пор, пока не достигнет узла, его содержащего. В этот момент переменная found будет установлена в True и условие while нарушится, что приведёт к возврату значения, как мы видели выше. Этот процесс можно рассмотреть на рисунке 10.
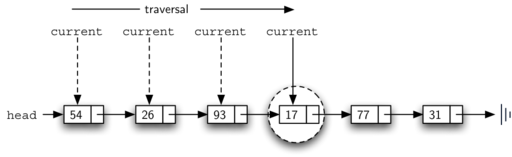
Рисунок 10: Успешный поиск значения 17
Метод remove логически требует двух стадий. Сначала надо обойти список, чтобы найти удаляемый элемент. Как только это случится (напомним, что мы предполагаем наличие искомого в списке), последует удаление. Первый шаг очень похож на search. Начиная с внешней ссылки, установленной на голову списка, мы обходим ссылки до тех пор, пока не найдём искомый элемент. Поскольку предполагается его присутствие, то цикл остановится до того, как current получит None. Следовательно, в условии можно ограничиться одной булевой переменной found.
Когда found примет значение True, current будет ссылаться на узел, содержащий элемент, который нужно удалить. Но как это сделать? Одним из способов является замена значения элемента неким маркером, обозначающим отсутствие элемента в списке. Проблемой при таком подходе является то, что теперь количество узлов не совпадает с количеством элементов. Было бы намного лучше удалять элемент с помощью удаления всего узла.
Для того, чтобы удалить нужный узел, нам нужно изменить ссылку его предшественника таким образом, чтобы она ссылалась на узел после current. К несчастью, не существует возможности перемещаться по связанному списку в обратном направлении. Поскольку current ссылается на узел следующий за тем, в котором мы хотели бы провести изменения, то для модификации уже слишком поздно.
Решением этой дилеммы станет использование двух внешних ссылок в процессе обхода списка. current будет вести себя как раньше, отмечая текущее положение обхода. Новая ссылка, которую мы назовём previous, будет всегда идти на один узел позади current. Таким образом, когда current остановится на удаляемом узле, previous будет указывать на место для соответствующей модификации связанного списка.
Листинг 7 демонстрирует метод remove полностью. В строках 2-3 двум ссылкам присваиваются начальные значения. Обратите внимание, что current начинает с головы списка, как в предыдущих примерах. Однако, предполагается, что previous всегда на узел позади текущего. По этой причине ей присваивается значение None, ведь не существует узла перед головой списка (см. рисунок 11). Булева переменная found вновь отвечает за контроль итераций.
В строках 6-7 мы спрашиваем, совпадает ли хранящийся в узле элемент с тем, который хотим удалить. Если да, то found устанавливается в True. Если нет, то previous и current перемещаются на один узел вперёд. Порядок двух присваиваний вновь очень важен. Прежде нужно переместить `previous, а затем current. Этот процесс часто называют “червяком”, так как previous должен догнать current до того, как тот вновь уйдёт вперёд. Рисунок 12 показывает перемещения previous и current в процессе спуска по списку в поисках узла, содержащего значение 17.
Листинг 7
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | def remove(self,item):
current = self.head
previous = None
found = False
while not found:
if current.getData() == item:
found = True
else:
previous = current
current = current.getNext()
if previous == None:
self.head = current.getNext()
else:
previous.setNext(current.getNext())
|
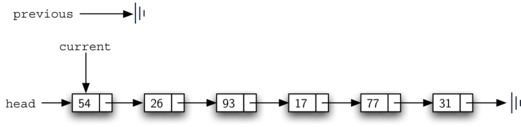
Рисунок 11: Начальные значения ссылок previous и current
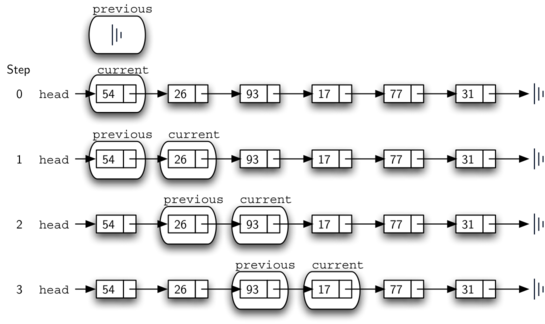
Рисунок 12: previous и current: вниз по списку
После завершения поискового шага метода remove нам нужно удалить узел из связанного списка. На рисунке 13 показана ссылка, которая должна быть изменена. Однако, есть особый случай, по которому требуется принять отдельное решение. Если удаляемый элемент - первый в списке, то current будет ссылаться на первый узел, а previous равен None. Ранее мы говорили, что указанием на узел, чья ссылка потребует изменения для завершения операции удаления, служит previous. Но в данном случае в модификации нуждается голова списка (см. рисунок 14).
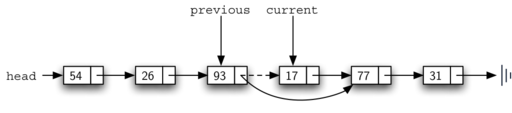
Рисунок 13: Удаление элемента из середины списка
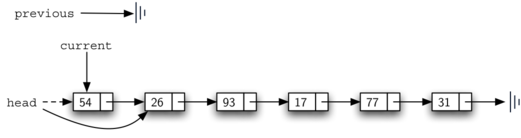
Рисунок 14: Удаление первого узла в списке
В строке 12 проверяется, имеем ли мы дело со специальным случаем, описанным выше. Если previous не перемещался, то он по-прежнему будет иметь значение None при found равном True. В этом случае (строка 13) голова списка изменяется так, чтобы ссылаться на узел, следующий за текущим, - эффект удаления первого узла из связанного списка. Однако, если previous не None, то удаляемый узел находится где-то ниже в связанном списке. В этом случае надо следовать основному алгоритму. Строка 15 использует метод setNext для previous, чтобы выполнить удаление. Отметьте, что в обоих случаях пункт назначения ссылки изменяется с помощью current.getNext(). Часто возникает такой вопрос: кроме двух уже рассмотренных случаев, как справиться с ситуацией, когда удаляемый элемент находится в последнем узле связанного списка? Мы оставляем на вас её рассмотрение.
Вы можете испытать класс UnorderedList в ActiveCode 1.
Полная реализация класса UnorderedList (unorderedlistcomplete)
Оставшиеся методы append, insert, index и pop остаются в качестве упражнений. Помните, что каждый из них должен учитывать место изменения: голова списка или его остаток. Также insert, index и pop требуют номера позиции в списке. Мы исходим из того, что нумерация индексов начинается с нуля.
Самопроверка
Часть I: Реализуйте метод `append` для неупорядоченного списка. Какова его временнАя сложность?
(self_check_list1)
Часть II: Скорее всего, вы создали append метод с \(O(n)\). Если вы добавите в класс UnorderedList некую переменную, то сможете сделать его с \(O(1)\). Будьте осторожны! Чтобы сделать это по-настоящему правильно, вам нужно рассмотреть несколько специальных случаев, которые могут потребовать модификации метода add.
(self_check_list2)