Инфиксные, префиксные и постфиксные выражения¶
Когда вы записываете арифметическое выражение вроде B * C, то его форма предоставляет вам достаточно информации для корректной интерпретации. В данном случае мы знаем, что переменная B умножается на переменную C, поскольку оператор умножения * находится в выражении между ними. Такой тип записи называется инфиксной, поскольку оператор расположен между (in between) двух операндов, с которыми он работает.
Рассмотрим другой инфиксный пример: A + B * C. Операторы + и * по-прежнему располагаются между операндами, но тут уже есть проблема. С какими именно операндами они будут работать? + работает с A и B или * принимает B и C? Выражение выглядит неоднозначно.
Фактически, вы можете читать и писать выражения такого типа долгое время, и они не будут вызывать у вас вопросов. Причина в том, что вы кое-что знаете о + и *. Каждый оператор имеет свой приоритет. Операторы с высоким приоритетом используются прежде операторов с низким. Единственной вещью, которая может изменить порядок приоритетов, являются скобки. Для арифметических операций умножение и деление стоят выше сложения и вычитания. Если появляются два оператора одинакового приоритета, то используются порядок слева направо, или их ассоциативность.
Давайте интерпретируем вызвавшее затруднение выражение A + B * C, используя приоритет операторов. B и C перемножаются первыми, затем к результату добавляется A. (A + B) * C заставит выполнить сложение A и B перед умножением. В выражении A + B + C по очерёдности (через ассоциативность) первым будет вычисляться самый левый +.
Хотя это очевидно для вас, помните: компьютер нуждается в точном знании того, как и в какой последовательности вычисляются операторы. Одним из способов записи выражения, гарантирующим, что не возникнет путаницы по отношению к порядку операций, является создание того, что называется выражением с полностью расставленными скобками. Такой тип выражения использует пару скобок для каждого оператора. Скобки диктуют порядок операций, так что здесь не возникает многозначности. Так же отпадает необходимость помнить правила расстановки приоритетов.
Выражение A + B * C + D может быть переписано как ((A + (B * C)) + D) с целью показать, что умножение происходит в первую очередь, а затем следует крайнее левое сложение. A + B + C + D перепишется в (((A + B) + C) + D), поскольку операции сложения ассоциируются слева направо.
Существует ещё два очень важных формата выражений, которые на первый взгляд могут показаться вам неочевидными. Рассмотрим инфиксную запись A + B. Что произойдёт, если мы поместим оператор перед двумя операндами? Результирующее выражение будет + A B. Также мы можем переместить оператор в конец, получив A B +. Всё это выглядит несколько странным.
Эти изменения позиции оператора по отношению к операндам создают два новых формата - префиксный и постфиксный. Префиксная запись выражения требует, чтобы все операторы предшествовали двум операндам, с которыми они работают. Постфиксная, в свою очередь, требует, чтобы операторы шли после соответствующих операндов. Несколько дополнительных примеров помогут прояснить этот момент (см. таблицу 2).
A + B * C в префиксной нотации можно переписать как + A * B C. Оператор умножения ставится непосредственно перед операндами B и C, указывая на приоритет * над +. Затем следует оператор сложения перед A и результатом умножения.
В постфиксной записи выражение выглядит как A B C * +. Порядок операций вновь сохраняется, поскольку * находится непосредственно после B и C, обозначая, что он имеет приоритет выше следующего +. Хотя операторы перемещаются и теперь находятся до или после соответствующих операндов, порядок последних по отношению друг к другу остаётся в точности таким, как был.
| Инфиксная запись | Префиксная запись | Постфиксная запись |
|---|---|---|
| A + B | + A B | A B + |
| A + B * C | + A * B C | A B C * + |
А сейчас рассмотрим инфиксное выражение (A + B) * C. Напомним, что в этом случае запись требует наличия скобок для указания выполнить сложение перед умножением. Однако, когда A + B записывается в префиксной форме, то оператор сложения просто помещается перед операндами: + A B. Результат этой операции является первым операндом для умножения. Оператор умножения перемещается в начало всего выражения, давая нам * + A B C. Аналогично, в постфиксной записи A B + явно указывается, что первым происходит сложение. Умножение может быть выполнено для получившегося результата и оставшегося операнда C. Соответствующим постфиксным выражением будет A B + C *.
Рассмотрим эти три выражения ещё раз (см. таблицу 3). Происходит что-то очень важное. Куда ушли скобки? Почему они не нужны нам в префиксной и постфиксной записи? Ответ в том, что операторы больше не являются неоднозначными по отношению к своим операндам. Только инфиксная запись требует дополнительных символов. Порядок операций внутри префиксного и постфиксного выражений полностью определён позицией операторов и ничем иным. Во многом именно это делает инфиксную запись наименее желательной нотацией для использования.
| Инфиксное выражение | Префиксное выражение | Постфиксное выражение |
|---|---|---|
| (A + B) * C | * + A B C | A B + C * |
Таблица 4 демонстрирует некоторые дополнительные примеры инфиксных выражений и эквивалентных им префиксных и постфиксных записей. Убедитесь, что вы понимаете, почему они эквивалентны с точки зрения порядка выполнения операций.
| Инфиксное выражение | Префиксное выражение | Постфиксное выражение |
|---|---|---|
| A + B * C + D | + + A * B C D | A B C * + D + |
| (A + B) * (C + D) | * + A B + C D | A B + C D + * |
| A * B + C * D | + * A B * C D | A B * C D * + |
| A + B + C + D | + + + A B C D | A B + C + D + |
Преобразование инфиксного выражения в префиксное и постфиксное¶
До сих пор мы использовали специальные методы для преобразования между инфиксными выражениями и эквивалентными им префиксной и постфикской записями. Как вы можете ожидать, существуют алгоритмические способы выполнения таких преобразований, позволяющие корректно трансформировать любое выражение любой сложности.
Первой из рассматриваемых нами техник будет использование идеи полной расстановки скобок в выражении, рассмотренной нами ранее. Напомним, что A + B * C можно записать как (A + (B * C)), чтобы явно показать приоритет умножения перед сложением. Однако, при более близком рассмотрении вы увидите, что каждая пара скобок также отмечает начало и конец пары операндов с соответствующим оператором по середине.
Взгляните на правую скобку в подвыражении (B * C) выше. Если мы передвинем символ умножения с его позиции и удалим соответствующую левую скобку, получив B C *, то произойдёт конвертирование подвыражение в постфиксную нотацию. Если оператор сложения тоже передвинуть к соответствующей правой скобке и удалить связанную с ним левую скобку, то результатом станет полностью постфиксное выражение (см. рисунок 6).
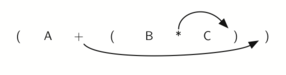
Рисунок 6: Перемещение операторов вправо для постфиксной записи
Если мы сделаем тоже самое, но вместо передвижения символа на позицию к правой скобке, сдвинем его к левой, то получим префиксную нотацию (см. рисунок 7). Позиция пары скобок на самом деле является ключом к окончательной позиции заключённого между ними оператора.
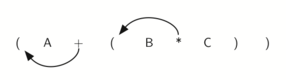
Рисунок 7: Перемещение операторов влево для префиксной записи.
Таким образом, при преобразовании выражения (неважно, насколько сложного) в префиксную или постфиксную запись для установления порядка выполнения операций используется полная расстановка скобок. Затем находящийся внутри них оператор передвигается на крайнюю левую или крайнюю правую позицию - в зависимости от того, префиксную или постфиксную запись вы хотите получить.
Вот более сложное выражение: (A + B) * C - (D - E) * (F + G). Рисунок 8 демонстрирует его преобразование в постфиксный и префиксный виды.
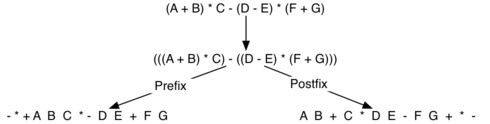
Рисунок 8: Преобразование сложного выражения к префиксной и постфиксной записи.
Обобщённое преобразование из инфиксного в постфиксный вид¶
Нам необходимо разработать алгоритм преобразования любого инфиксного выражения в постфиксное. Для этого посмотрим ближе на сам процесс конвертирования.
Рассмотрим ещё раз выражение A + B * C. Как было показано выше, его постфиксным эквивалентом является A B C * +. Мы уже отмечали, что операнды A, B и C остаются на своих местах, а местоположение меняют только операторы. Ещё раз взглянем на операторы в инфиксном выражении. Первым при проходе слева направо нам попадётся +. Однако, в постфиксном выражении + находится в конце, так как следующий оператор, *, имеет приоритет над сложением. Порядок операторов в первоначальном выражении обратен результирующему постфиксному выражению.
В процессе обработки выражения операторы должны где-то храниться, пока не найден их соответствующий правый операнд. Также порядок этих сохраняемых операторов может быть обратным (из-за их приоритета), как в данном примере со сложением и умножением. Поскольку оператор сложения, появляющийся перед оператором умножения, имеет более низкий приоритет, то он должен появиться после использования последнего. Из-за такого обратного порядка имеет смысл рассмотреть использование стека для хранения операторов до тех пор, пока они не понадобятся.
Что насчёт (A + B) * C? Напомним его постфиксный эквивалент: A B + C *. Повторимся, что обрабатывая это инфиксное выражение слева направо, первым мы встретим +. В этом случае, когда мы увидим *, + уже будет помещён в результирующее выражение, поскольку имеет преимущество над * в силу использования скобок. Теперь можно приступить к рассмотрению работы алгоритма преобразования. Когда мы видим левую скобку, то сохраняем её как знак, что должен будет появиться другой оператор с высоким приоритетом. Он будет ожидать, пока не появится соответствующая правая скобка, чтобы отметить его местоположение (вспомните технику полной расстановки скобок). После появления правой скобки оператор выталкивается из стека.
Поскольку мы сканируем инфиксное выражение слева направо, то для хранения операторов будем использовать стек. Это предоставит нам обратный порядок, который был отмечен в первом примере. На вершине стека всегда будет последний сохранённый оператор. Когда бы мы не прочитали новый оператор, мы должны сравнить его по приоритету с операторами в стеке (если таковые имеются).
Предположим, что инфиксное выражение есть строка токенов, разделённых пробелами. Токенами операторов являются *, /, + и - вместе с правой и левой скобками, ( и ). Токены операндов - это однобуквенные идентификаторы A, B, C и так далее. Следующая последовательность шагов даст строку токенов в постфиксном порядке.
- Создать пустой стек с названием opstack для хранения операторов. Создать пустой список для вывода.
- Преобразовать инфиксную строку в список, используя строковый метод split.
- Сканировать список токенов слева направо.
- Если токен является операндом, то добавить его в конец выходного списка.
- Если токен является левой скобкой, положить его в opstack.
- Если токен является правой скобкой, то выталкивать элементы из opstack пока не будет найдена соответствующая левая скобка. Каждый оператор добавлять в конец выходного списка.
- Если токен является оператором *, /, + или -, поместить его в opstack. Однако, перед этим вытолкнуть любой из операторов, уже находящихся в opstack, если он имеет больший или равный приоритет, и добавить его в результирующий список.
#. Когда входное выражение будет полностью обработано, проверить opstack. Любые операторы, всё ещё находящиеся в нём, следует вытолкнуть и добавить в конец итогового списка.
Рисунок 9 демонстрирует алгоритм преобразования, работающий над выражением A * B + C * D. Заметьте, что первый оператор * удаляется до того, как мы встречаем оператор +. Также + остаётся в стеке, когда появляется второй *, поскольку умножение имеет приоритет перед сложением. В конце инфиксного выражения из стека дважды происходит выталкивание, удаляя оба оператора и помещая + как последний элемент в результирующее постфиксное выражение.
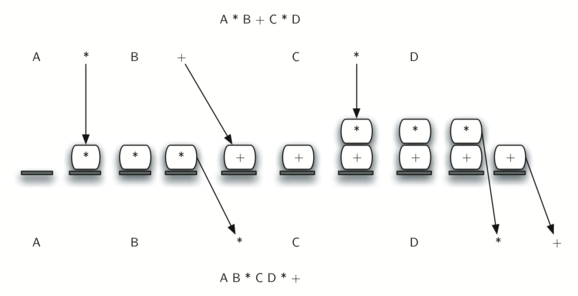
Рисунок 9: Преобразование A * B + C * D в постфиксную запись
Чтобы закодировать алгоритм на Python, мы будем использовать словарь под именем prec для хранения значений приоритета операторов. Он связывает каждый оператор с целым числом, которые можно сравнивать с числами других операторов, как уровень приоритетности (для этого мы произвольно выбрали целые числа 3, 2 и 1). Левая скобка получит самое низкое значение. Таким образом, любой сравниваемый с ней оператор будет иметь приоритет выше и располагаться над ней. Строка 15 определяет, что операнды могут быть любыми символами в верхнем регистре или цифрами. Полная функция преобразования показана в ActiveCode 8.
Преобразование инфиксного выражения в постфиксное (intopost)
Ниже показаны ещё несколько примеров выполнения этой функции.
>>> infixtopostfix("( A + B ) * ( C + D )")
'A B + C D + *'
>>> infixtopostfix("( A + B ) * C")
'A B + C *'
>>> infixtopostfix("A + B * C")
'A B C * +'
>>>
Постфиксные вычисления¶
В последнем примере использования стека мы рассмотрим вычисление выражения, которое уже находится в постфиксной форме. В этом случае структурой для решения задачи вновь выбран стек. Однако, поскольку вы сканируете постфиксное выражение, ждать своей очереди должны уже операнды, а не операторы, в противоположность алгоритму выше. Ещё один способ думать об этом решении: когда на входе обнаружится оператор, для вычисления будут использованы два самых последних операнда.
Чтобы разобраться в этом более детально, рассмотрим постфиксное выражение 4 5 6 * +. Сканируя его слева направо, вы прежде всего натолкнётесь на операнды 4 и 5. Что с ними делать неизвестно, пока не известен следующий символ. Помещение каждого из них в стек гарантирует их доступность на случай, если следующим появится оператор.
В нашем случае следующий символ - ещё один операнд. Так что мы, как и раньше, помещаем его в стек и проверяем следующий символ. Видим оператор *, что означает перемножение двух самых последних операндов. Сделав выталкивание из стека дважды, получим необходимые множители, а затем выполним умножение (в данном случае результатом будет 30).
Теперь можно обработать полученное значение, поместив его обратно в стек, чтобы оно могло использоваться в качестве операнда для последующих операторов в выражении. Когда будет обработан последний оператор, в стеке останется только одно значение. Выталкиваем его и возвращаем как результат выражения. Рисунок 10 демонстрирует содержание стека на протяжении всего процесса вычисления выражения из примера.
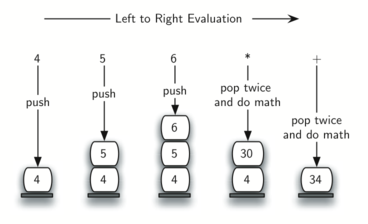
Рисунок 10: Содержание стека в процессе вычисления
На рисунке 11 показан несколько более сложный пример: 7 8 + 3 2 + /. Здесь есть два момента, которые стоит отметить. Первый: размер стека возрастает, уменьшается и вновь растёт в процессе вычисления подвыражений. Второй: обрабатывать оператор деления нужно очень внимательно. Напомним, что операнды в постфиксном выражении идут в их изначальном порядке, поскольку постфикс меняет только положение оператора. Когда операнды деления выталкиваются из стека, они находятся в обратной последовательности. Поскольку деление не коммутативный оператор (другими словами, \(15/5\) не то же самое, что \(5/15\)), мы должны быть уверены, что порядок операндов не изменился.
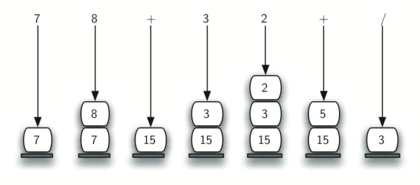
Рисунок 11: Более сложный пример вычисления
Предположим, что постфиксное выражение - это строка токенов, разделённых пробелами. Операторами являются *, /, + и -, а под операндами понимаются одноразрядные целые значения. На выходе будет целочисленный результат.
- Создаём пустой стек под названием operandStack.
- Преобразовываем строку в список, используя строковый метод split.
- Сканируем список токенов слева направо.
- Если токен является операндом, то преобразовываем его из строки в целое число и помещаем значение в operandStack.
- Если токен является оператором *, /, + или -, то он нуждается в двух операндах. Производим выталкивание из operandStack дважды. Сначала вытолкнется второй операнд, а затем - первый. Выполняем арифметическую операцию и помещаем результат обратно в operandStack.
- Когда входное выражение полностью обработано, его результат находится в стеке. Выталкиваем его из operandStack и возвращаем в качестве ответа.
Полностью функция для вычисления постфиксных выражений показана в ActiveCode 9. Для помощи с арифметикой определена вспомогательная функция doMath. Она принимает два операнда и оператор, после чего совершает надлежащую арифметическую операцию.
Постфиксное вычисление (postfixeval)
Важно отметить, что для обеих программ - постфиксного преобразования и постфиксного вычисления - мы предполагаем отсутствие ошибок во входном выражении. Используя эти программы, как точку отсчёта, вы можете легко увидеть, как в них могут быть включены определение ошибок и сообщение об этом. Мы оставляем это как упражнение в конце главы.
Самопроверка