Симуляция: Задания на печать¶
Более интересная симуляция позволит нам изучить поведение очереди на печать, описанной ранее в этом разделе. Напомним, что когда студенты отправляют документы для печати на общем принтере, то задания помещаются в очередь, чтобы быть обработанными в манере “первым пришёл - первым обслужен”. В связи с такого рода конфигурацией возникает много вопросов. Возможно, наиболее важный из них: способен ли принтер обработать определённое количество документов? Если нет, то студенты будут ждать чересчур долго и могут пропустить следующую лекцию.
Рассмотрим такую ситуацию в лаборатории информатики. В любой среднестатистический день в любой час здесь работает порядка 10 студентов. В течение этого времени они обычно печатают дважды, причём длина задания варьируется от одной до двадцати страниц. Принтер в лаборатории стар и в черновом качестве способен обрабатывать всего 10 страниц в минуту. Можно переключить его на лучшее качество печати, но тогда производительность упадёт до 5 страниц/мин. Низкая скорость печати заставляет студентов ждать слишком долго. Какую скорость для страниц следует использовать?
Мы можем определить это, построив симуляционную модель лаборатории. Нам потребуется создать представления студентов, заданий на печать и принтера (рисунок 4). Когда студенты подают документы на печать, мы будем добавлять их в список ожидания - очередь заданий на печать, прикреплённую к принтеру. Когда принтер заканчивает очередное задание, он смотрит в очередь на предмет наличия оставшихся документов для обработки. Интерес для нас представляет среднее время ожидания задачи в очереди.
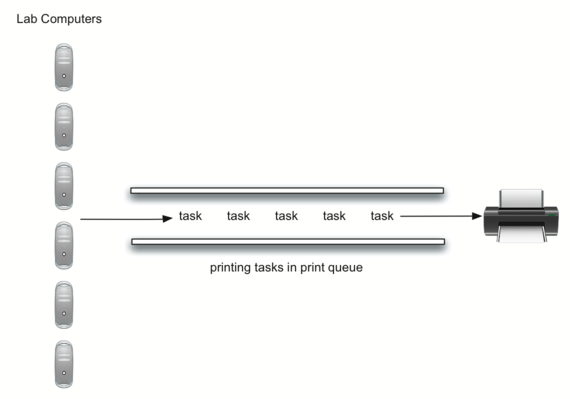
Рисунок 4: Очередь на печать в лаборатории информатики
Для моделирования этой ситуации нам нужно использовать некоторые вероятности. Например, студенты могут печатать документы размером от одной до двадцати страниц. Если каждая длина от 1 до 20 одинаково возможна, то текущий размер задания на печать можно симулировать, используя случайное число от 1 до 20 включительно. Это означает, что шансы возникновения документа любой длины от 1 до 20 равны.
Если в лаборатории находятся десять студентов и каждый из них печатает дважды, то в среднем в час будет 20 заданий на печать. Какова вероятность, что в любую заданную секунду одно из них будет создано? Способ ответить на этот вопрос - рассмотреть отношение количества заданий ко времени. Двадцать заданий на час означают одно задание на каждые 180 секунд:
\(\frac {20\ tasks}{1\ hour} \times \frac {1\ hour} {60\ minutes} \times \frac {1\ minute} {60\ seconds}=\frac {1\ task} {180\ seconds}\)
Для каждой секунды мы можем симулировать вероятность появления задания путём генерации случайного числа между 1 и 180 включительно. Если число равно 180, то мы говорим, что задание создано. Заметьте, что возможно создание множества заданий одного за другим или наоборот - мы можем ждать долгое время, пока что-то появится. Такова природа моделирования. Желательно симулировать реальную ситуацию настолько близко к реальности, насколько это возможно, учитывая всё, что известно об общих параметрах.
Основные шаги симуляции¶
Вот основная модель.
- Создать очередь из заданий на печать. Каждое из них будет иметь отметку о времени постановки в очередь. В самом начале очередь пуста.
- Для каждой секунды (currentSecond):
- Создано ли новое задание на печать? Если да, то добавить его в очередь с currentSecond в качестве отметки времени.
- Если принтер не занят и есть ожидающее задание, то
- Удалить следующее задание из очереди на печать и передать его принтеру.
- Извлечь отметку о времени из currentSecond чтобы вычислить время ожидания для данного задания.
- Добавить время ожидания этой задачи в список для дальнейшей обработки.
- Основываясь на количестве страниц в задании на печать, вычислить, сколько для него потребуется времени.
- Если необходимо, принтер тратит одну секунду печати. Также он вычитает её из времени, необходимого для выполнения задачи.
- Если задание завершено (другими словами, требуемое на его выполнение время равно нулю), то принтер более не занят.
- После завершения симуляции вычисляется среднее время ожидания из сгенерированного списка времён ожидания.
Реализация на Python¶
Для этой симуляции мы создадим классы трёх объектов реального мира, описанных выше: Printer, Task, и PrintQueue.
Классу Printer (листинг 2) будет необходима возможность отслеживать, имеет ли он текущую задачу. Если да, то он занят (строки 13-17), и необходимо вычислить временнЫе затраты, исходя из количества страниц в задании. Так же конструктор позволяет инициализировать настройку количества печатаемых в минуту страниц. Метод tick уменьшает на единицу внутренний таймер и устанавливает холостой ход принтера (строка 11), если задание выполнено.
Листинг 2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | class Printer:
def __init__(self, ppm):
self.pagerate = ppm
self.currentTask = None
self.timeRemaining = 0
def tick(self):
if self.currentTask != None:
self.timeRemaining = self.timeRemaining - 1
if self.timeRemaining <= 0:
self.currentTask = None
def busy(self):
if self.currentTask != None:
return True
else:
return False
def startNext(self,newtask):
self.currentTask = newtask
self.timeRemaining = newtask.getPages() * 60/self.pagerate
|
Класс заданий (листинг 3) будет представлять единичное задание для печати. Когда оно создаётся, генератор случайных чисел предоставляет его длину в диапазоне от 1 до 20 страниц. Мы выбрали использование функции randrange из модуля random.
>>> import random
>>> random.randrange(1,21)
18
>>> random.randrange(1,21)
8
>>>
Так же каждое задание нуждается в отметке, которая будет использоваться для подсчёта времени ожидания. Она будет представлять из себя момент, когда задание было создано и помещено в очередь принтера. Затем может быть использован метод waitTime для извлечения времени, затраченного на ожидание в очереди начала печати.
Листинг 3
import random
class Task:
def __init__(self,time):
self.timestamp = time
self.pages = random.randrange(1,21)
def getStamp(self):
return self.timestamp
def getPages(self):
return self.pages
def waitTime(self, currenttime):
return currenttime - self.timestamp
Основная симуляция (листинг 4) воплощает алгоритм, описанный выше. Объект printQueue представляет собой экземпляр нашего существующего АТД очереди. Вспомогательная булева функция newPrintTask определяет, было ли создано новое задание на печать. Мы вновь выбрали функцию randrange из модуля random, чтобы возвращать случайное целое из диапазона от 1 до 180. Задания на печать появляются раз в каждые 180 секунд. Произвольно выбрав 180 из диапазона целых чисел (строка 32), мы можем симулировать это случайное событие. Функция симуляции позволяет нам установить для принтера общее время и количество страниц в минуту.
Листинг 4
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 | from pythonds.basic.queue import Queue
import random
def simulation(numSeconds, pagesPerMinute):
labprinter = Printer(pagesPerMinute)
printQueue = Queue()
waitingtimes = []
for currentSecond in range(numSeconds):
if newPrintTask():
task = Task(currentSecond)
printQueue.enqueue(task)
if (not labprinter.busy()) and (not printQueue.isEmpty()):
nexttask = printQueue.dequeue()
waitingtimes.append(nexttask.waitTime(currentSecond))
labprinter.startNext(nexttask)
labprinter.tick()
averageWait=sum(waitingtimes)/len(waitingtimes)
print("Average Wait %6.2f secs %3d tasks remaining."%(averageWait,printQueue.size()))
def newPrintTask():
num = random.randrange(1,181)
if num == 180:
return True
else:
return False
for i in range(10):
simulation(3600,5)
|
При запуске симуляции нас не должно беспокоить, что результаты каждый раз будут разными. Это заложено в вероятностную природу случайных чисел. Нас больше интересуют тенденции, которые появляются при корректировке параметров симуляции. Вот некоторые результаты.
В первый раз мы запускаем симуляцию для периода в 60 минут (3600 секунд), используя скорость печати 5 страниц в минуту. Дополнительно проводим 10 независимых попыток. Помните, что поскольку симуляция работает со случайными числами, то на каждом запуске получатся разные результаты.
>>>for i in range(10):
simulation(3600,5)
Average Wait 165.38 secs 2 tasks remaining.
Average Wait 95.07 secs 1 tasks remaining.
Average Wait 65.05 secs 2 tasks remaining.
Average Wait 99.74 secs 1 tasks remaining.
Average Wait 17.27 secs 0 tasks remaining.
Average Wait 239.61 secs 5 tasks remaining.
Average Wait 75.11 secs 1 tasks remaining.
Average Wait 48.33 secs 0 tasks remaining.
Average Wait 39.31 secs 3 tasks remaining.
Average Wait 376.05 secs 1 tasks remaining.
После запуска десяти попыток мы видим, что среднее время ожидания составляет 122,155 секунд. Так же заметен большой разброс средних весов времени от 17,27 до максимальных 376,05 секунд. Обратите внимание, что задания завершили выполнение всего в двух случаях.
А теперь установим скорость печать на 10 страниц в минуту и вновь запустим 10 попыток. С большей скоростью мы можем надеяться выполнить больше заданий в рамках одного часа.
>>>for i in range(10):
simulation(3600,10)
Average Wait 1.29 secs 0 tasks remaining.
Average Wait 7.00 secs 0 tasks remaining.
Average Wait 28.96 secs 1 tasks remaining.
Average Wait 13.55 secs 0 tasks remaining.
Average Wait 12.67 secs 0 tasks remaining.
Average Wait 6.46 secs 0 tasks remaining.
Average Wait 22.33 secs 0 tasks remaining.
Average Wait 12.39 secs 0 tasks remaining.
Average Wait 7.27 secs 0 tasks remaining.
Average Wait 18.17 secs 0 tasks remaining.
Вы можете запустить симуляцию самостоятельно в ActiveCode 2.
Симуляция очереди принтера (qumainsim)
Обсуждение¶
Мы пытались ответить на вопрос, может ли текущий принтер обработать загруженное задание, если установлена печать лучшего качества, но с более низкой скоростью. Подход, который использовался для написания симуляции, моделировал задания на печать, как случайные события различной длины и времени появления.
Вывод выше показывает, что с пятью страницами в минуту среднее время ожидания варьируется от 17 до 376 секунд (около шести минут). С более высокой скоростью печати нижним значением становится одна секунда, а верхним - всего 28. Более того, в 8 из 10 запусков при 5 страниц/мин по истечение часа в очереди остаются ожидающие задания.
Таким образом, мы, убедились, что снижение скорости печати в пользу улучшения качества - не самая лучшая идея. Студенты не могут позволить себе так долго ждать свои документы, особенно когда им надо спешить на следующую пару. Шестиминутное ожидание будет просто чересчур долгим.
Такой тип анализа симуляции позволяет нам ответить на множество вопросов, в целом известных как “что, если?”. Всё, что нужно - это менять параметры, используемые для симуляции, и тогда мы можем моделировать любое количество интересных случаев. Например,
- Что, если возрастёт среднее число принятых заявок на печать, а среднее количество студентов увеличится до 20 человек?
- Что, если сегодня суббота, и студентам не нужно идти на занятия? Могут ли они позволить себе ожидание?
- Что, если размер среднего задания на печать уменьшится, поскольку Python - очень мощный язык, и программы на нём имеют тенденцию становиться короче?
На все эти вопросы можно ответить, модифицируя симуляцию выше. Однако, важно помнить, что модель хороша настолько, насколько хороши допущения, на которых она построена. Для создания надёжной модели были необходимы настоящие данные о числе заданий на печать и количестве студентов в час.
Самопроверка
Как бы вы модифицировали симуляцию принтера, чтобы отразить большее число студентов? Предположим, что оно удвоилось. Вам необходимо сделать некоторые разумные допущения о том, как связать это с данной моделью. Что бы вы изменили? Переделайте код. Также предположите, что длина среднего задания на печать уменьшилась в половину. Измените код, чтобы отразить это. Наконец, как бы вы параметризировали количество студентов? Вместо того, чтобы каждый раз изменять код, мы бы предпочли просто задавать число студентов параметром симуляции.
(print_sim_selfcheck)