Построение графа для “словесной лестницы”¶

Наша первая задача: выяснить, как можно преобразовать в граф большую коллекцию слов. Мы хотели бы иметь ребро от одного слова к другому, если они различаются всего в единственной букве. С таким графом любой путь от одного слова к другому станет решением головоломки. Рисунок 1 показывает маленький граф из слов, решающий словесную лестницу от FOOL к SAGE. Обратите внимание, что граф ненаправленный и все его рёбра имеют одинаковый вес.

Рисунок 1: Маленький граф для “словесной лестницы”.

Мы можем использовать несколько подходов для решения задачи по созданию графа. Начнём с предположения, что у нас есть список из слов одинаковой длины. В качестве стартовой точки, из каждого его элемента можно создать вершину графа. Чтобы выяснить связи между ними, можно сравнивать каждое слово в списке со всеми прочими. Мы будем смотреть на количество различающихся букв. Если два слова отличаются всего в одной букве, то между ними будет создано ребро графа. Для небольшого набора слов этот метод сработает очень хорошо. Однако, предположим, что наш список содержит 5 110 слов. Говоря приблизительно, сравнение каждого слова с каждым означает \(O(n^2)\) алгоритм. Для 5 110 слов это даст больше 26 миллионов сравнений.

Можно поступить лучше, используя следующий подход. Предположим, у нас есть огромное количество корзин, на каждой из которых написано четырёхбуквенное слово, в котором одна буква заменена подчёркиванием. Для примера рассмотрим рисунок 2: у нас есть корзина с меткой “pop_.” При обработке каждого слова в списке мы сравниваем его с корзинами, используя ‘_’ для произвольной подстановки. Таким образом, с “pop_.” можно связать и “pope”, и “pops”. Каждый раз, когда находится связь с корзиной, мы кладём в неё слово. Когда слова разложены, всё, лежащее в одной корзине, должно быть связано между собой.

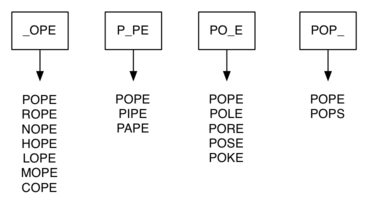
Рисунок 2: Корзины для слов, отличающихся всего в одной букве.

В Python описанную схему можно реализовать с помощью словаря. Метки на корзинах будут ключами, а хранимым значением станет список слов. И раз уж у нас построен словарь, то мы можем создать и граф. Начнём с создания вершины для каждого слова, а затем проведём рёбра между всеми вершинами, чьи слова имеют в словаре одинаковый ключ. Листинг 1 показывает код на Python, необходимый для построения такого графа.

Листинг 1

from pythonds.graphs import Graph

def buildGraph(wordFile):
    d = {}
    g = Graph()
    wfile = open(wordFile,'r')
    # create buckets of words that differ by one letter
    for line in wfile:
        word = line[:-1]
        for i in range(len(word)):
            bucket = word[:i] + '_' + word[i+1:]
            if bucket in d:
                d[bucket].append(word)
            else:
                d[bucket] = [word]
    # add vertices and edges for words in the same bucket
    for bucket in d.keys():
        for word1 in d[bucket]:
            for word2 in d[bucket]:
                if word1 != word2:
                    g.addEdge(word1,word2)
    return g

Поскольку это наша первая задача на графы из реального мира, вам может быть любопытно, насколько разрежен результат. Имеющийся список четырёхбуквенных слов для неё содержит 5 110 элементов. Если бы мы использовали матрицу смежности, то в ней было бы 5 110 * 5 110 = 26 112 100 ячеек. Граф, построенный функцией buildGraph имеет ровно 53 286 рёбер, так что матрица была бы заполнена только на 0.2%! Вот уж действительно очень разреженная матрица.