Алгоритм Прима для остовного дерева¶
Предлагаем для нашего последнего алгоритма на графах рассмотреть задачу, с которой часто сталкиваются разработчики онлайн игр и провайдеры интернет-радио. Проблема в том, что им нужно эффективно передавать информационные пакеты для всех и каждого, кто может её услышать. Это важно в играх, поскольку все игроки должны знать последний ход каждого из них. Это важно для интернет-радио, потому что настроенные на него слушатели должны получить все данные, по которым можно было бы воссоздать прослушиваемую песню. Задача о вещании проиллюстрирована рисунком 9.
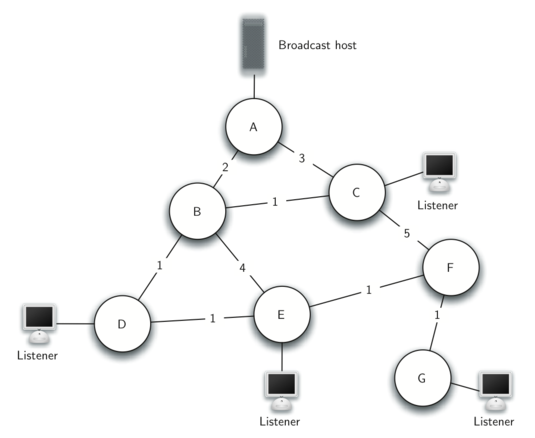
Рисунок 9: Задача о вещании
Существует несколько способов её решения путём непосредственного перебора. С них мы и начнём, чтобы лучше разобраться в вопросе. Так же это поможет вам оценить решение, которое мы в итоге предложим. Начнём с того, что станция вещания имеет некую информацию, которая должна быть передана всем слушателям. Простейшим решением станет хранить список всех слушателей и отсылать им индивидуальные сообщения. На рисунке 9 показана небольшая сеть с передатчиком и несколько слушателей. Используя первый подход, следует отправлять по четыре копии каждого сообщения. Предполагая, что используется путь с наименьшими затратами, давайте посмотрим, сколько времени каждый маршрутизатор потратит на расылку одинаковых сообщений.
Все сообщения от вещателя идут через маршрутизатор А, поэтому он “видит” по четыре копии каждого. Маршрутизатор С “видит” уже по одной из них, однако, для B и D это число равно трём, поскольку через них проходят кратчайшие пути к слушателям 1, 2 и 3. С учётом того, что для радиовещания станция должен расслылать сотни сообщений каждую секунду, получается огромный объём лишнего трафика.
Метод перебора состоит в том, что станция вещания посылает единственную копию сообщения и позволяет маршрутизаторам дальше разбираться самим. В этом случае простейшим решением станет стратегия под названием неконтролируемое наводнение. Работает она так. Каждое сообщение выпускается с временем жизни, или ttl (от англ. time to live - прим. переводчика), установленным в некоторую величину, большую или равную количеству рёбер между станцией вещания и наиболее удалённым слушателем. Каждый маршрутизатор получает копию сообщения и рассылает его всем своим соседям, уменьшив ttl на единицу. Те, в свою очередь, поступают аналогично. Так продолжается до тех пор, пока значение ttl не станет равным нулю. Можно легко убедиться, что неконтролируемое наводнение генерирует намного больше ненужных сообщений, чем наша первая стратегия.
Решение задачи лежит в создании остовного дерева с минимальным весом. Формальное определение минимального остовного дерева \(T\) для графа \(G = (V,E)\) следующее: \(T\) - это ацикличное подмножество \(E\), соединяющее все вершины в \(V\). Сумма весов рёбер в \(T\) - минимальна.
Рисунок 10 показывает упрощённую версию графа вещания и выделяет рёбра его минимального остовного дерева. Теперь, чтобы решить задачу вещания, станция просто направляет единственную копию сообщения в сеть. Каждый из маршрутизаторов пересылает его тому своему соседу, который является частью остовного дерева, за исключеннием источника посылки. В нашем примере А перешлёт сообщение В, В - C и D. D отправит сообщение E, который передаст его F, а тот - G. Никто из маршрутизаторов не “увидит” больше одной копии сообщения, а все слушатели смогут его услышать.
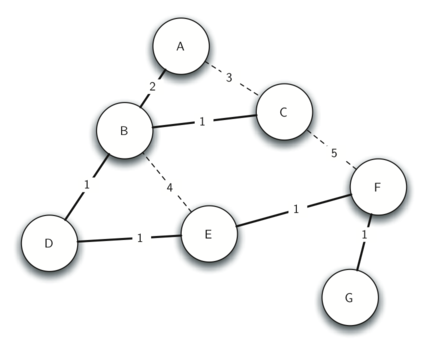
Рисунок 10: Минимальное остовное дерево графа вещания
Алгоритм, который мы используем для решения этой задачи, называется алгоритмом Прима. Он входит в семейство под названием “жадные алгоритмы”, поскольку на каждом шаге выбирается наименее затратный из предлагаемых путей. В данном случае таковым будет перемещение по ребру с наименьшим весом. Наше последнее задание: реализовать алгоритм Прима.
Основная идея для создания остовного дерева состоит в следующем:
Пока T не остовное дерево
Найти ребро, которое можно безопасно добавить к дереву
Добавить новое ребро в T
Загвоздка состоит в пункте “найти ребро для безопасного добавления”. Определим безопасное ребро как то, которое соединяет вершину из остовного дерева с вершиной вне его. Это гарантирует, что дерево всегда останется деревом и не будет иметь циклов.
Код на Python для реализации алгоритма Прима показан в листинге 2. Он похож на алгоритм Дейкстры в том, что оба они используют очередь с приоритетом для выбора следующей вершины, которая будет добавлена в растущий граф.
Листинг 2
from pythonds.graphs import PriorityQueue, Graph, Vertex
def prim(G,start):
pq = PriorityQueue()
for v in G:
v.setDistance(sys.maxsize)
v.setPred(None)
start.setDistance(0)
pq.buildHeap([(v.getDistance(),v) for v in G])
while not pq.isEmpty():
currentVert = pq.delMin()
for nextVert in currentVert.getConnections():
newCost = currentVert.getWeight(nextVert) \
+ currentVert.getDistance()
if nextVert in pq and newCost<nextVert.getDistance():
nextVert.setPred(currentVert)
nextVert.setDistance(newCost)
pq.decreaseKey(nextVert,newCost)
Следующие рисунки (с 11 по 17) демонстрируют работу алгоритма с простым деревом из примера. Начинаем с вершины А. Для всех прочих вершин расстояние инициализированно бесконечностью. Рассмотрев соседей А, мы обновляем значения пути двух дополнительных вершин В и С, поскольку расстояние до них через А меньше бесконечности. Это перемещает В и С в начало очереди с приоритетом. Обновляем у этих узлов ссылки на предшественника, установив их на А. Важно отметить, что формально мы ещё не добавили В и С в остовное дерево. Узел не считается его частью, пока он не удалён из очереди с приоритетом.
Поскольку В имеет наименьшее расстояние, следующим рассматриваем его. Проверка соседей В показывает, что пути D и E можно обновить. Оба этих узла получают новые значения расстояний и обновлённые ссылки на предшественника. Перемещаясь к следующему узлу по очереди с приоритетом, мы обнаруживаем С. Единственный смежный с ним узел, который до сих пор находится в очереди, - это F. Следовательно, мы можем обновить расстояние до него и отрегулировать его позицию в очереди.
Теперь проверяем вершины, смежные с узлом D. Обнаруживаем, что можем обновить Е и уменьшить его расстояние с 6 до 4. Когда мы делаем это, ссылка на предшественника Е устанавливается в D, что подготавливает узел к добавлению в остовное дерево (правда, на другую позицию). Оставшаяся часть алгоритма действует так, как от неё ожидается, добавляя в дерево каждый новый узел.
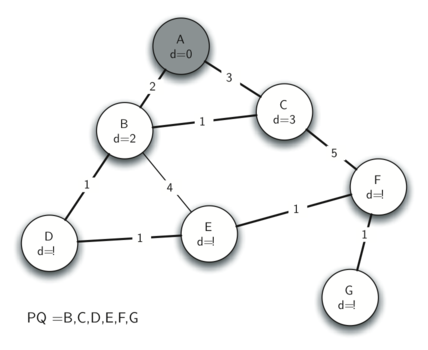
Рисунок 11: Трассировка алгоритма Прима
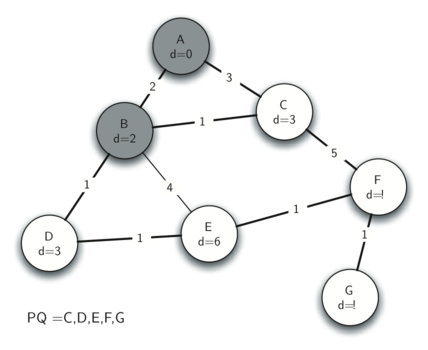
Рисунок 12: Трассировка алгоритма Прима
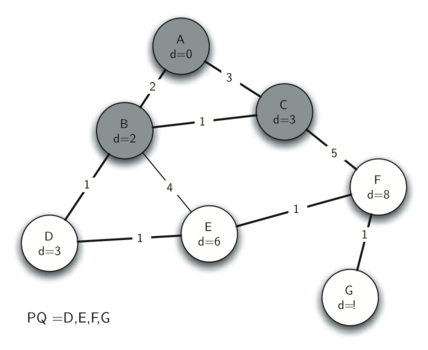
Рисунок 13: Трассировка алгоритма Прима
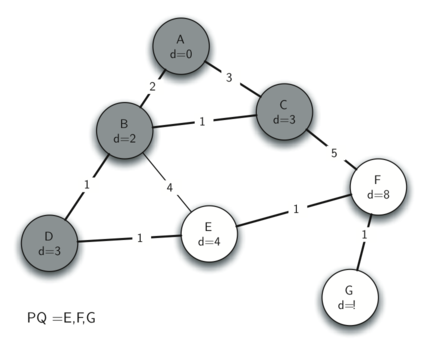
Рисунок 14: Трассировка алгоритма Прима
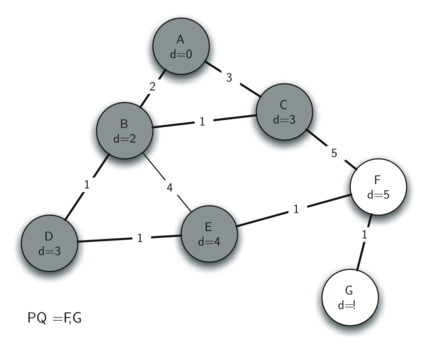
Рисунок 15: Трассировка алгоритма Прима
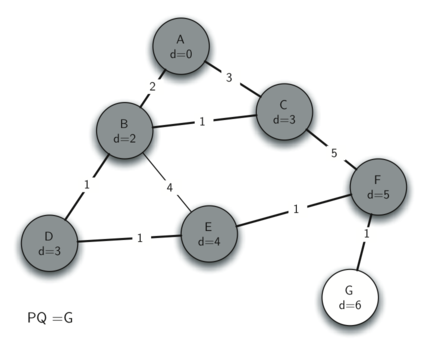
Рисунок 16: Трассировка алгоритма Прима
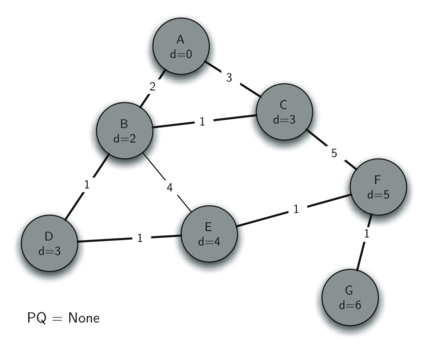
Рисунок 17: Трассировка алгоритма Прима