Сильно связные компоненты¶
В оставшейся части этой главы мы обратим наше внимание на очень большие графы. Чтобы изучить несколько дополнительных алгоритмов, будем использовать графы связей между хостами в интернете и ссылок между веб-страницами.
Поисковые системы вроде Google и Bing используют в своих интересах тот факт, что страницы в вебе образуют очень большой направленный граф. Чтобы преобразовать в него Всемирную Паутину, мы будем рассматривать страницы, как вершины, а гиперссылки между ними - как соединяющие их рёбра. Рисунок 30 демонстрирует очень маленькую часть графа, получившегося из ссылок от одной страницы к другой со стартовой точкой на домашней странице Luther College’s Computer Science. Конечно, этот граф был бы огромным, так что мы ограничили его сайтами, на которые есть не более десяти ссылок с домашней страницы CS.
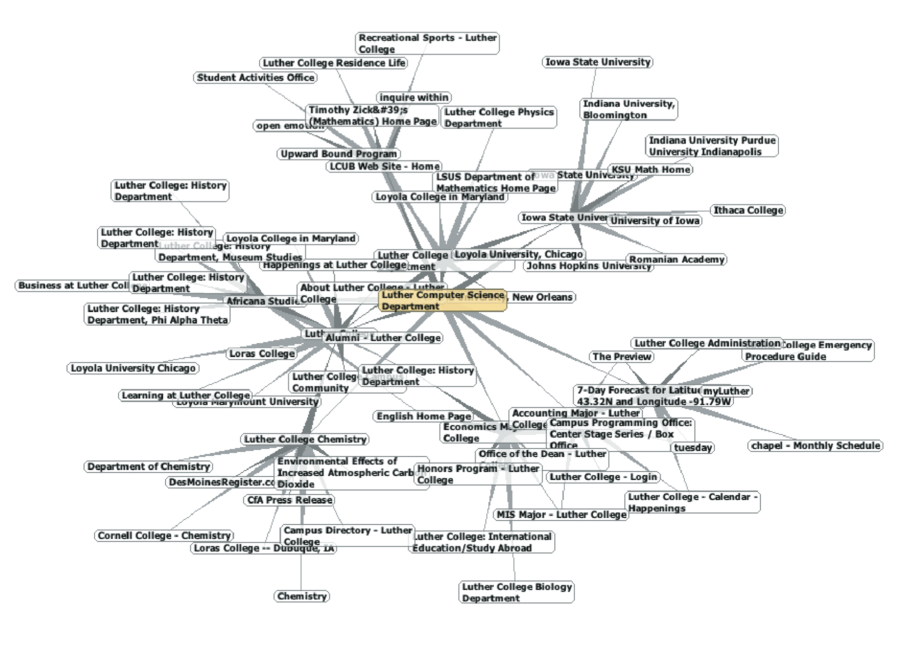
Рисунок 30: Граф из ссылок с домашней страницы Luther Computer Science
Если вы изучите граф на рисунке 30, то сможете сделать несколько любопытных наблюдений. Во-первых, многие из веб-сайтов графа - прочие сайты Luther College. Во-вторых, в графе присутствует несколько ссылок на колледж в Айове. В-третьих, в нём имеется несколько ссылок на другие гуманитарные колледжи. Из этого можно сделать заключение, что здесь присутствует некая внутренняя структура, объединяющая вместе сайты, в чём-то похожие друг на друга.
Один из алгоритмов, помогающих найти кластеры из сильно связных вершин графа, называется алгоритмом поиска сильно связных компонентов, или SCC (от англ. strongly connected components - прим. переводчика). Формально мы можем определить сильно связную компоненту, \(C\) графа \(G\), как наибольшее подмножество вершин \(C \subset V\) таких, что для каждой пары \(v, w \in C\) существует путь от \(v\) до \(w\) и от \(w\) до \(v\). На рисунке 27 показан простой граф с тремя сильно связными компонентами, которые выделены разными затенёнными областями.
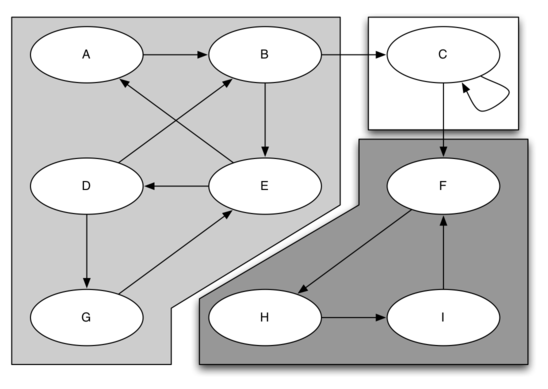
Рисунок 31: Направленный граф с тремя сильно связными компонентами
После определения сильно связных компонент, мы можем показать упрощённый вид графа, собрав все вершины каждой из них в одну большую. Упрощённая версия графа с рисунка 31 показана на рисунке 32.
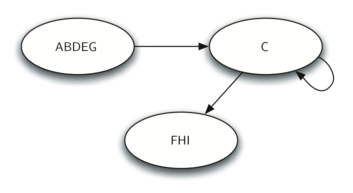
Рисунок 32: Упрощённый граф
Вновь мы видим, что, используя поиск в глубину, можем создать очень мощный и эффективный алгоритм. Однако, прежде нужно рассмотреть ещё одно определение. Транспозиция графа \(G\) определяется, как граф \(G^T\), у которого все рёбра имеют обратное направление. Т.е., если в оригинальном графе ребро направлено из узла А в узел В, то \(G^T\) будет содержать ребро из узла В в узел А.
Рисунки 33 и 34 демонстрируют простой граф и его транспозицию.
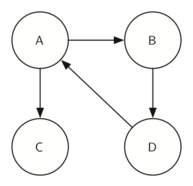
Figure 33: Граф \(G\)
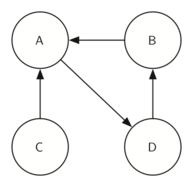
Figure 34: Его транспозиция \(G^T\)
Посмотрите ещё раз на рисунки. Обратите внимание, что граф на рисунке 33 имеет две сильно связные компоненты. А теперь взгляните на рисунок 34. На нём так же изображены две сильно связные компоненты.
Теперь мы можем описать алгоритм вычисления SCC в графе.
- Вызвать dfs для графа \(G\), чтобы вычислить “времена” выхода каждой вершины.
- Вычислить \(G^T\).
- Вызвать dfs для графа \(G^T\), но в основном цикле DFS исследовать каждую вершину в порядке убывания “времени” выхода.
- Каждое дерево из леса, найденного на шаге 3, будет сильно связной компонентой. Для её идентификации осталось вывести id каждого узла всех деревьев в лесу.
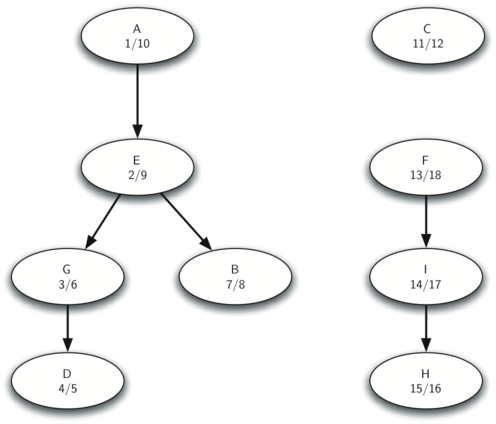
Давайте пошагово проследим описанные выше пункты для графа на рисунке 31. Рисунок 35 показывает “времена” входа и выхода, вычисленные для оригинального графа с помощью алгоритма DFS. На рисунке 36 показаны они же, но вычисленные для транспозиции графа.
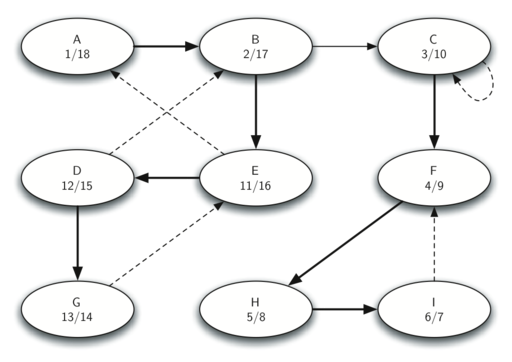
Рисунок 35: “Времена” выхода для графа \(G\)
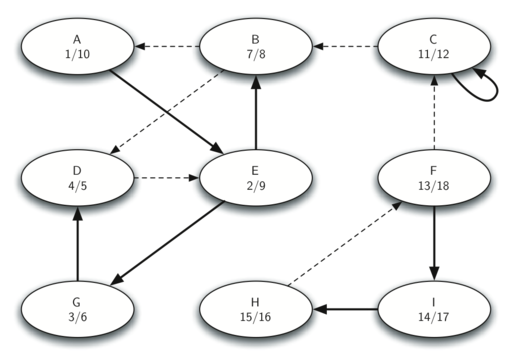
Рисунок 36: “Времена” выхода для \(G^T\)
Наконец, на рисунке 37 показан лес из трёх деревьев, созданный SCC алгоритмом на третьем шаге. Заметьте, что мы не даём вам код на Python для этого алгоритма, поскольку его написание остаётся в качестве упражнения.