Терминология и определения¶

А сейчас, после знакомства с несколькими примерами, давайте дадим более формальное определение графу и его компонентам. С некоторыми из терминов мы уже сталкивались при обсуждении деревьев.

Вершина

Вершина (иногда её называют “узел”) - основная часть графа. Может иметь имя, которое называется “ключ”. Также вершина может обладать дополнительной информацией, которую мы будем называть “полезной нагрузкой”.

Ребро

Ребро (или “дуга”) - другая фундаментальная часть графа. Ребро, соединяющее две вершины, показывает наличие между ними определённых отношений. Рёбра могут быть одно- и двунаправленными. Если все рёбра графа однонаправленные, то мы называем его направленным графом или диграфом (от англ. directed graph - прим. переводчика). Показанный выше граф необходимых для профилирования предметов - явный диграф, поскольку вы обязаны проходить одни курсы прежде, чем другие.

Вес

Рёбра могут иметь вес, показывающий стоимость перемещения от одной вершины к другой. Например, в графе дорог, связывающих города, вес ребра может отображать расстояние между двумя населёнными пунктами.

Имея на руках все эти формулировки, мы способны дать формальное определение графа. Он может быть представлен как \(G\), где \(G =(V,E)\). Здесь \(V\) - множество вершин графа, а \(E\) - множество соединяющих их рёбер. Каждое ребро представляет собой кортеж \((v,w)\), где \(w,v \in V\). Сюда можно добавлять третий компонент, отображающий вес ребра. Подграф \(s\) - это набор рёбер \(e\) и вершин \(v\) таких, что \(e \subset E\) и \(v \subset V\).

Рисунок 2 демонстрирует ещё один пример простого диграфа с весами. Формально мы можем представить его, как множество из шести вершин:

и множество из девяти рёбер:

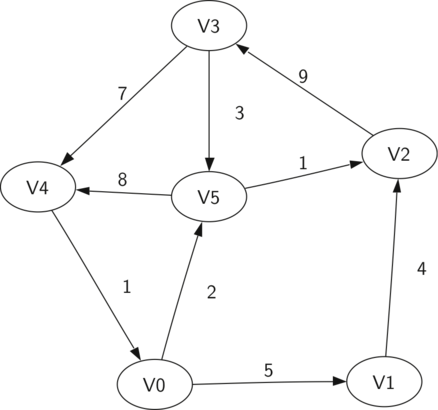
Рисунок 2: Простой пример направленного графа.

Пример графа на рисунке 2 помогает проиллюстрировать два других ключевых темина графа:

Путь

Путь в графе - это последовательность вершин, соединённых рёбрами. Формально путь можно определить, как \(w_1, w_2, ..., w_n\) такой, что \((w_i, w_{i+1}) \in E\) для всех \(1 \le i \le n-1\).

Длиной пути без весов станет количество в нём рёбер: \(n-1\). Взвешенный путь в графе будет суммой весов всех входящих в него рёбер. Например, на рисунке 2 путём из \(V3\) в \(V1\) является последовательность вершин \((V3,V4,V0,V1)\). Рёбрами - \(\left\{(v3,v4,7),(v4,v0,1),(v0,v1,5) \right\}\).

Цикл

Цикл в направленном графе начинается и заканчивается в одной и той же вершине. Например, на рисунке 2 циклом будет путь \((V5,V2,V3,V5)\). Граф без циклов называется ацикличным. Направленный граф без циклов - это “ациклический направленный граф” или DAG (от англ. directed acyclic graph - прим. переводчика). Мы увидим, что с его помощью можно решить некоторые важные задачи.