Объектно-ориентированное программирование в Python: определение классов¶

Класс Fraction¶

Очень распространённым примером для демонстрации деталей реализации пользовательского класса является разработка класса, воплощающего АТД Fraction. Мы уже видели, что Python предоставляет в наше пользование несколько числовых классов. Однако, бывают моменты, когда более подходящим является создание объекта данных лишь “выглядящего как” дробь.

Дробь (например, \(\frac {3}{5}\)) состоит из двух частей. Верхнее значение, называемое числитель, может быть любым целым числом. Нижнее значение (знаменатель) - любым целым, большим нуля (отрицательные дроби имеют отрицательный числитель). Также для любой дроби можно создать приближение с плавающей запятой. В этом случае мы хотели бы представлять дробь как точное значение.

Операции для типа Fraction будут позволять его объектам данных вести себя подобно любым другим числовым значениям. Мы должны быть готовы складывать, вычитать, умножать и делить дроби. Также необходима возможность показывать дроби в их стандартной “слэш”-форме (например, \(\frac {3}{5}\)). Все методы дробей должны возвращать результат в своей сокращённой форме таким образом, чтобы, вне зависимости от вида вычислений, в конце мы всегда имели наиболее общепринятую форму.

В Python мы определяем новый класс предоставлением его имени и набора определений методов, которые синтаксически подобны определениям функций. В этом примере

class Fraction:

   #методы писать тут

нам дан каркас для определения методов. Первым из них (его должны предоставлять все классы) является конструктор. Он определяет способ создания объекта данных. Чтобы создать объект Fraction, нам нужно предоставить два элемента данных - числитель и знаменатель. В Python метод конструктора всегда называется __init__ (по два подчёркивания до и после init). Он демонстрируется в листинге 2:

Листинг 2

class Fraction:

    def __init__(self,top,bottom):

        self.num = top
        self.den = bottom

Обратите внимание, что список формальных параметров содержит три элемента (self, top, bottom). self - это специальный параметр, который используется, как обратная ссылка на сам объект. Он всегда должен быть первым формальным параметром, однако, при вызове конструктора в него никогда не передаётся актуальное значение. Как было написано ранее, дробям нужны данные для двух частей - числителя и знаменателя. Нотация self.num конструктора определяет, что объект fraction имеет внутренний объект данных, именуемый num, как часть своего состояния. Аналогично, self.den создаёт знаменатель. Значения этих двух формальных параметров изначально устанавливаются в состояние, позволяющее новому объекту fraction знать своё начальное значение.

Чтобы создать сущность класса Fraction, мы должны вызвать конструктор. Это произойдёт при использовании имени класса с подстановкой актуальных значений в необходимое состояние (заметьте, что мы никогда не вызываем непосредственно __init__). Например,

myfraction = Fraction(3,5)

создаст объект с именем myfraction, представляющий дробь \(\frac {3}{5}\) (три пятых). Рисунок 5 показывает этот объект, как уже существующий.

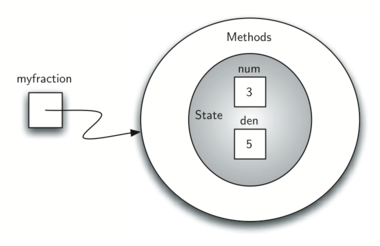
Рисунок 5: Экземпляр класса Fraction

Следующее, чем мы займёмся, это реализация поведения, требуемого абстрактным классом. Для начала рассмотрим, что происходит, когда мы пытаемся напечатать объект Fraction.

>>> myf = Fraction(3,5)
>>> print(myf)
<__main__.Fraction instance at 0x409b1acc>

Объект fraction, myf не знает, как ему отвечать на запрос о печати. Функция print требует, чтобы объект конвертировал самого себя в строку, которая будет записана на выходе. Единственный выбор, который имеет myf, - это показать актуальную ссылку, хранящуюся в переменной (непосредственный адрес). Это явно не то, что мы хотим.

Существует два пути решения этой проблемы. Первый - определить метод под названием show, который позволит объекту Fraction печать самого себя как строку. Мы можем реализовать его, как показано в листинге 3. Если создавать объект Fraction как и раньше, то можно попросить его показать себя (другими словами, напечатать себя) в подходящем формате. К сожалению, в общем случае это не будет работать. Для того, чтобы организовать печать должным образом, нам необходимо сообщить классу Fraction, как ему конвертировать себя в строку. Это то, что необходимо функции print для нормальной работы.

Листинг 3

def show(self):
     print(self.num,"/",self.den)

>>> myf = Fraction(3,5)
>>> myf.show()
3 / 5
>>> print(myf)
<__main__.Fraction instance at 0x40bce9ac>
>>>

В Python у всех классов имеется набор стандартных методов, которые предоставляются по умолчанию, но могут не работать должным образом. Один из них, __str__, - метод преобразования объекта в строку. Реализация по умолчанию для этого метода, как мы уже могли видеть, возвращает строку адреса экземпляра класса. Что нам необходимо сделать, так это предоставить для него “лучшую” реализацию. Мы будем говорить, что она перегружает предыдущую (или переопределяет поведение метода).

Для этого просто определим метод с именем __str__ и зададим ему новую реализацию, как показано в листинге 4. Это определение не нуждается ни в какой дополнительной информации, кроме специального параметра self. В свою очередь, метод будет создавать строковое представление конвертированием каждого кусочка внутренних данных состояния в строку и конкатенацией этих строк с помощью символа / между ними. Результирующая строка будет возвращаться всякий раз, как объект Fraction попросит преобразовать себя в строку. Обратите внимание на различные способы использования этой функции.

Листинг 4

def __str__(self):
    return str(self.num)+"/"+str(self.den)

>>> myf = Fraction(3,5)
>>> print(myf)
3/5
>>> print("I ate", myf, "of the pizza")
I ate 3/5 of the pizza
>>> myf.__str__()
'3/5'
>>> str(myf)
'3/5'
>>>

Мы можем перегрузить множество других методов для нашего нового класса Fraction. Одними из наиболее важных из них являются основные арифметические операции. Мы хотели бы иметь возможность создать два объекта Fraction, а затем сложить их вместе, используя стандартную запись “+”. На данный момент, складывая две дроби, мы получаем следующее:

>>> f1 = Fraction(1,4)
>>> f2 = Fraction(1,2)
>>> f1+f2

Traceback (most recent call last):
  File "<pyshell#173>", line 1, in -toplevel-
    f1+f2
TypeError: unsupported operand type(s) for +:
          'instance' and 'instance'
>>>

Если вы внимательнее посмотрите на сообщение об ошибке, то заметите - загвоздка в том, что оператор “+” не понимает операндов Fraction.

Мы можем исправить это, предоставив классу Fraction метод, перегружающий сложение. В Python он называется __add__ и принимает два параметра. Первый - self- необходим всегда, второй представляет из себя второй операнд выражения. Например,

f1.__add__(f2)

будет запрашивать у Fraсtion объекта f1 прибавить к нему Fraction объект f2. Это может быть записано и в стандартной нотации f1 + f2.

Для того, чтобы сложить две дроби, их нужно привести к общему знаменателю. Простейший способ увериться, что у них одинаковый знаменатель, - это использовать в его качестве произведение знаменателей дробей. Т.е. \(\frac {a}{b} + \frac {c}{d} = \frac {ad}{bd} + \frac {cb}{bd} = \frac{ad+cb}{bd}\) Реализация показана в листинге 5. Функция сложения возвращает новый объект Fraction с числителем и знаменателем суммарной дроби. Мы можем использовать этот метод при написании стандартных арифметических выражений с дробями, присваивая результату суммарную дробь и выводя её на экран.

Листинг 5

def __add__(self,otherfraction):

     newnum = self.num*otherfraction.den + self.den*otherfraction.num
     newden = self.den * otherfraction.den

     return Fraction(newnum,newden)

>>> f1=Fraction(1,4)
>>> f2=Fraction(1,2)
>>> f3=f1+f2
>>> print(f3)
6/8
>>>

Метод сложения работает, как мы того и хотели, но одну вещь можно было бы улучшить. Заметьте, что 6/8 - это правильный результат вычисления (1/4 + 1/2), но это не сокращённая форма. Лучшим представлением будет 3/4. Для того, чтобы быть уверенными, что результат всегда имеет сокращённый вид, нам понадобится вспомогательная функция, умеющая сокращать дроби. В ней нужно будет находить наибольший общий делитель, или НОД. Затем мы сможем разделить числитель и знаменатель на НОД, а результат и будет сокращением до наименьших членов.

Наиболее известный алгоритм нахождения наибольшего общего делителя - это алгоритм Евклида, который будет детально обсуждаться в главе 8. Он устанавливает, что наибольшим общим делителем двух чисел m и n будет n, если m делится на n нацело. Однако, если этого не происходит, то ответом будет НОД n и остатка деления m на n. Мы просто предоставим здесь итеративную реализацию этого алгоритма (см. ActiveCode 11). Обратите внимание, что она работает только при положительном знаменателе. Это допустимо для нашего класса дробей, поскольку мы говорили, что отрицательные дроби будут представляться отрицательным числителем.

Теперь можно использовать эту функцию для сокращения любой дроби. Чтобы представить дробь в сокращённом виде, мы будем делить числитель и знаменатель на их наибольший общий делитель. Итак, для дроби \(6/8\) НОД равен 2. Разделив верх и низ на 2, мы получим новую дробь \(3/4\) (см. листинг 6).

Листинг 6

def __add__(self,otherfraction):
    newnum = self.num*otherfraction.den + self.den*otherfraction.num
    newden = self.den * otherfraction.den
    common = gcd(newnum,newden)
    return Fraction(newnum//common,newden//common)

>>> f1=Fraction(1,4)
>>> f2=Fraction(1,2)
>>> f3=f1+f2
>>> print(f3)
3/4
>>>

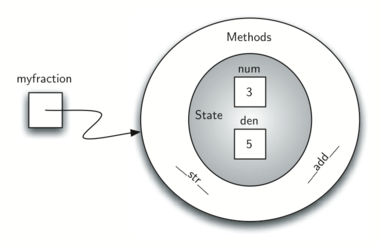
Рисунок 6: Экземпляр класса Fraction с двумя методами

Сейчас наш объект Fraction имеет два очень полезных метода и выглядит, как показано на Рисунке 6. Группа дополнительных методов, которые нам понадобится включить в класс Fraction, содержит способ сравнивать две дроби. Предположим, что у нас есть два объекта Fraction f1 и f2. f1 == f2 будет истиной, если они ссылаются на один и тот же объект. Два разных объекта с одинаковыми числителями и знаменателями в этой реализации равны не будут. Это называется поверхностным равенством (см. рисунок 7)

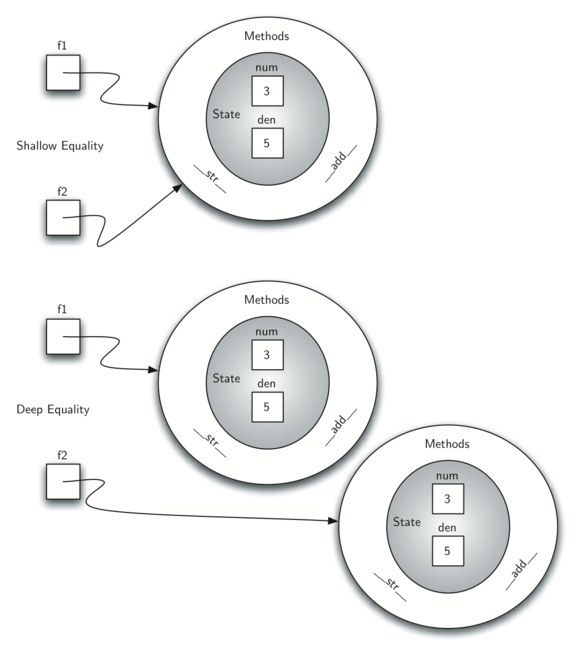
Рисунок 7: Поверхностное равенство vs глубокое равенство

Мы можем создать глубокое равенство (см. рисунок 7) - по одинаковому значению, а не по одинаковой ссылке - перегрузив метод __eq__. Это ещё один стандартный метод, доступный в любом классе. Он сравнивает два объекта и возвращает True, если их значения равны, или False в противном случае.

В классе Fraction мы можем реализовать метод __eq__, вновь представив обе дроби в виде с одинаковым знаменателем и затем сравнив их числители (см. листинг 7). Здесь также важно отметить другие операторы отношений, которые могут быть перегружены. Например, метод __le__ предоставляет функционал “меньше или равно”.

Листинг 7

def __eq__(self, other):
    firstnum = self.num * other.den
    secondnum = other.num * self.den

    return firstnum == secondnum

Полностью класс Fraction, реализованный на данный момент, показан в ActiveCode 12. Мы оставляем читателям оставшуюся арифметику и методы отношений в качестве упражнений.

Наследование: логические вентили и схемы¶

Наш финальный раздел будет посвящён другому важному аспекту объектно-ориентированного программирования. Наследование - это способность одного класса быть связанным с другим классом подобно тому, как бывают связаны между собой люди. Дети наследуют черты своих родителей. Аналогично, в Python класс-потомок наследует характеристики данных и поведения от класса-предка. Такие классы часто называют субклассами и суперклассами, соответственно.

Рисунок 8 показывает встроенные коллекции Python и взаимоотношения между ними. Такого рода структуру отношений называют иерархией наследования. Например, список является потомком коллекций с последовательным доступом. В данном случае мы назовём список “наследником”, а коллекцию - “родителем” (или список - субклассом, коллекцию - суперклассом). Такая зависимость часто называется отношением IS-A (список является (is a) коллекцией с последовательным доступом). Это подразумевает, что списки наследуют важнейшие характеристики коллекций, в частности - упорядочение исходных данных, и такие операции, как конкатенация, повторение и индексация.

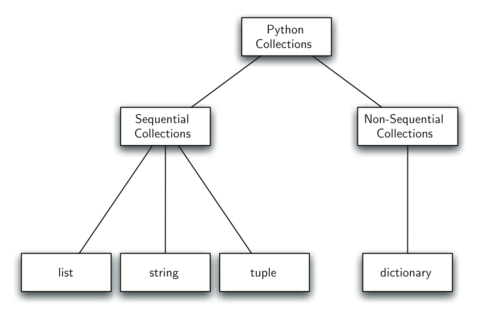
Рисунок 8: Иерархия наследования для коллекций Python

И списки, и кортежи, и строки представляют из себя коллекции с последовательным доступом, наследуя общую организацию данных и операции. Однако, они различны по гомогенности данных и мутабельности наборов. Все потомки наследуют своим родителям, но различаются между собой включением дополнительных характеристик.

Организовывая классы в иерархическом порядке, объектно-ориентированные языки программирования позволяют расширять ранее написанный код под вновь возникающие потребности. В дополнение, организовывая данные в иерархической манере, мы лучше понимаем существующие между ними взаимоотношения. Мы можем создавать более эффективное абстрактное представление.

Чтобы глубже исследовать эту идею, мы напишем симуляцию - приложение, симулирующее цифровые цепи. Её основными строительными блоками будут логические элементы. Эти электронные переключатели представляют собой соотношения булевой алгебры между их входом и выходом. В общем случае вентили имеют единственную линию выхода. Значение на ней зависит от значений, подаваемых на входные линии.

Вентиль “И” (AND) имеет два входа, на каждый из которых может подаваться нуль или единица (кодирование False или True, соответственно). Если на оба входа подана единица, то значение на выходе тоже 1. Однако, если хотя бы один из входов установлен в нуль, то результатом будет 0. Вентиль “ИЛИ” также имеет два входа и выдаёт единицу, если хотя бы на одном из них 1. В случае, когда обе входные линии в нуле, результат тоже 0.

Вентиль “НЕ” (NOT) отличается от предыдущих тем, что имеет всего один вход. Значение на выходе будет просто обратным входному значению. Т.е., если на входе 0, то на выходе 1, и наоборот. Рисунок 9 показывает, как обычно представляют каждый из этих вентилей. Так же каждый из них имеет свою таблицу истинности значений, отражающую отображение вентилем входа на выход.

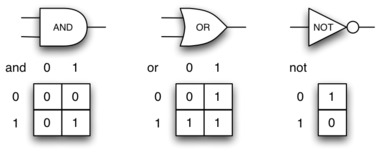
Рисунок 9: Три типа логических элементов

Комбинируя эти вентили в различные структуры и применяя к полученному наборы входных комбинаций, мы можем строить цепи, обладающие различными логическими функциями. Рисунок 10 демонстрирует цепь, состоящую из двух вентилей “И”, одного вентиля “ИЛИ” и одного вентиля “НЕ”. Выходы элементов “И” подключены непосредственно к входам элемента “ИЛИ”, а его результирующий вывод - ко входу вентиля “НЕ”. Если мы будем подавать набор входных значений на четыре входные линии (по две на каждый элемент “И”), то они будут обработаны, и результат появится на выходе вентиля “НЕ”. Рисунок 10 так же демонстрирует пример со значениями.

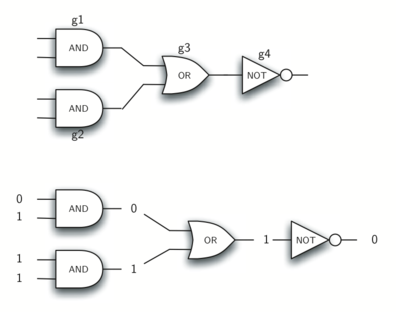
Рисунок 10: Цепь

Задавшись целью воплотить эту цепь, мы прежде всего должны создать представление для логических вентилей. Их легко организовать, как класс с наследственной иерархией, показанной на Рисунке 11. Верхний класс LogicGate представляет наиболее общие характеристики логических элементов: в частности, метку вентиля и линию выхода. Следующий уровень субклассов разбивает логические элементы на два семейства: имеющие один вход и имеющие два входа. Ниже уже появляются конкретные логические функции для каждого вентиля.

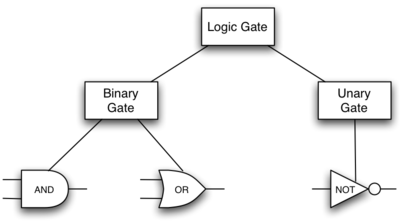
Рисунок 11: Иерархия наследования для логических элементов

Теперь мы можем заняться реализацией классов, начиная с наиболее общего - LogicGate. Как уже отмечалось ранее, каждый вентиль имеет метку для идентификации и единственную линию выхода. В дополнение, нам потребуются методы, позволяющие пользователю запрашивать у вентиля его метку.

Следующим аспектом поведения, в котором нуждается любой вентиль, является необходимость знать его выходное значение. Это требуется для выполнения вентилями соответствующих алгоритмов, основанных на текущих значениях на входах. Для генерации выходного значения логическим элементам необходимо конкретное знание логики их работы. Это подразумевает вызов метода, совершающего логические вычисления. Полностью класс показан в листинге 8

Листинг 8

class LogicGate:

    def __init__(self,n):
        self.label = n
        self.output = None

    def getLabel(self):
        return self.label

    def getOutput(self):
        self.output = self.performGateLogic()
        return self.output

На данный момент мы не будем реализовывать функцию performGateLogic. Причина в том, что мы не знаем, как будут работать логические операции у каждого вентиля. Эти детали мы включим для каждого добавленного в иерархию элемента индивидуально. Это очень мощная идея объектно-ориентированного программирования: мы пишем метод, который будет использовать ещё не существующий код. Параметр self является ссылкой на актуальный вентиль, вызывающий метод. Любые вновь добавленные в иерархию логические элементы просто будут нуждаться в собственной реализации функции performGateLogic, которая станет использоваться в нужный момент. После этого вентили должны предоставить своё выходное значение. Эта возможность расширять существующую иерархию и обеспечивать необходимые для её нового класса функции чрезвычайно важна для повторного использования существующего кода.

Мы разделили логические элементы, основываясь на количестве их входных линий. У вентиля “И” их две, как и у вентиля “ИЛИ”, а у вентиля “НЕ” - одна. Класс BinaryGate будет субклассом LogicGate и включит в себя элементы с двумя входными линиями. Класс UnaryGate также будет субклассом LogicGate, но входная линия у его элементов будет одна. В конструировании компьютерных цепей такие линии иногда называют “пинами”, так что мы будем использовать эту терминологию и в нашей реализации.

Листинг 9

class BinaryGate(LogicGate):

    def __init__(self,n):
        LogicGate.__init__(self,n)

        self.pinA = None
        self.pinB = None

    def getPinA(self):
        return int(input("Enter Pin A input for gate "+ self.getLabel()+"-->"))

    def getPinB(self):
        return int(input("Enter Pin B input for gate "+ self.getLabel()+"-->"))

Листинг 10

class UnaryGate(LogicGate):

    def __init__(self,n):
        LogicGate.__init__(self,n)

        self.pin = None

    def getPin(self):
        return int(input("Enter Pin input for gate "+ self.getLabel()+"-->"))

Листинг 9 и листинг 10 реализуют эти два класса. Конструкторы обоих начинаются с явного вызова конструктора родительского класса с использованием метода __init__. Когда мы создаём экземпляр класса BinaryGate, то прежде всего хотим инициализировать любые элементы данных, которые наследуются от LogicGate. В данном случае это метка вентиля. Затем конструктор добавляет два входа (pinA и pinB). Это очень распространённая схема, которую вам следует использовать при проектировании иерархии классов. Конструктору дочернего класса сначала нужно вызвать конструктор родительского класса, и только потом переключаться на собственные, отличные от предка, данные.

Единственным, что добавится к поведению класса BinaryGate будет возможность получать значения от двух входных линий. Поскольку они берутся откуда-то извне, то с помощью оператора ввода мы можем просто попросить пользователя предоставить их. То же самое происходит в реализации класса UnaryGate, за исключением того момента, что он имеет всего один вход.

Теперь, когда у нас есть общие классы для вентилей, зависящие от количества их входов, мы можем создавать специфические вентили с уникальным поведением. Например, класс AndGate, который будет подклассом BinaryGate, поскольку элемент “И” имеет два входа. Как и раньше, первая строка конструктора вызывает конструктор базового класса (BinaryGate), который, в свою очередь, вызывает конструктор своего родителя (LogicGate). Обратите внимание, что класс AndGate не предоставляет каких-либо новых дополнительных данных, поскольку наследует две входные линии, одну выходную и метку.

Листинг 11

class AndGate(BinaryGate):

    def __init__(self,n):
        BinaryGate.__init__(self,n)

    def performGateLogic(self):

        a = self.getPinA()
        b = self.getPinB()
        if a==1 and b==1:
            return 1
        else:
            return 0

Единственная вещь, которую необходимо добавить в AndGate, - это специфическое поведение при выполнении булевых операций, которое мы описывали выше. Это то место, где мы можем предоставить метод performGateLogic. Для вентиля “И” он сначала должен получить два входных значения и вернуть 1, если оба они равны единице. Полностью данный класс показан в листинге 11.

Мы можем продемонстрировать работу класса AndGate`, создав его экземпляр и попросив его вычислить своё выходное значение. Следующий код показывает AndGate-объект g1, который имеет внутреннюю метку "G1". Когда мы вызываем метод getOutput, объект сначала должен вызвать свой метод performGateLogic, который, в свою очередь, запрашивает значения из двух входных линий. После того, как требуемые данные получены, показывается правильное выходное значение.

>>> g1 = AndGate("G1")
>>> g1.getOutput()
Enter Pin A input for gate G1-->1
Enter Pin B input for gate G1-->0
0

Такая же работа должна быть проведена для элементов “ИЛИ” и “НЕ”. Класс OrGate также будет субклассом BinaryGate, а класс NotGate расширит UnaryGate. Оба они будут нуждаться в собственной реализации функции performGateLogic со специфическим поведением.

Мы можем использовать единичный логический элемент, сконструировав в начале экземпляр одного из классов вентилей и затем запросив его выходное значение (что, в свою очередь, потребует предоставления входных данных). Например,

>>> g2 = OrGate("G2")
>>> g2.getOutput()
Enter Pin A input for gate G2-->1
Enter Pin B input for gate G2-->1
1
>>> g2.getOutput()
Enter Pin A input for gate G2-->0
Enter Pin B input for gate G2-->0
0
>>> g3 = NotGate("G3")
>>> g3.getOutput()
Enter Pin input for gate G3-->0
1

Теперь, когда у нас есть работающие базовые вентили, мы можем вернуться к построению цепей. Чтобы создать цепь, нам необходимо соединить вентили вместе: выход одного ко входу другого. Для мы реализуем новый класс под названием Connector.

Класс Connector не будет принадлежать иерархии логических элементов. Однако, он будет использовать её, поскольку каждый соединитель имеет два вентиля - по одному на каждый конец (см. рисунок 12). Отношения такого рода очень важны в объектно-ориентированном программировании. Они называются отношениями “HAS-A”. Напомним, что ранее мы использовали словосочетание “IS-A отношение”, чтобы показать, как дочерний класс относится к родительскому. Например, UnaryGate является (IS-A) LogicGate.

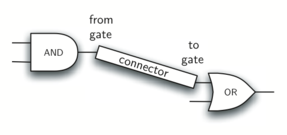
Рисунок 12: Connector соединяет выход одного вентиля со входом другого.

Теперь для класса Connector мы скажем, что он имеет LogicGate, подразумевая, что соединители имеют внутри экземпляры LogicGate, но не являются частью иерархии. При конструировании классов очень важно различать те из них, которые имеют отношения “IS-A” (что требует наследования), и те, которые обладают отношениями “HAS-A” (без наследования).

Листинг 12 демонстрирует класс Connector. Два экземпляра вентилей внутри каждого объекта соединителя будут обозначаться как fromgate и togate, различая таким образом, что данные будут “течь” от выхода одного вентиля ко входу другого. Вызов setNextPin очень важен при создании соединителей (см. листинг 13). Нам необходимо добавить этот метод к нашим классам для вентилей таким образом, чтобы каждый togate мог выбрать подходящую входную линию для соединения.

Листинг 12

class Connector:

    def __init__(self, fgate, tgate):
        self.fromgate = fgate
        self.togate = tgate

        tgate.setNextPin(self)

    def getFrom(self):
        return self.fromgate

    def getTo(self):
        return self.togate

В классе BinaryGate для вентилей с двумя возможными входными линиями коннектор должен присоединяться только к одной из них. Если доступны обе, то по умолчанию мы будем выбирать pinA. Если он уже подсоединён к чему-либо, то выберем pinB. Подсоединиться к вентилю, не имеющему доступных входов, невозможно.

Листинг 13

def setNextPin(self,source):
    if self.pinA == None:
        self.pinA = source
    else:
        if self.pinB == None:
            self.pinB = source
        else:
           raise RuntimeError("Error: NO EMPTY PINS")

Теперь можно получать входные данные двумя способами: извне, как раньше, и с выхода вентиля, присоединённого ко входу данного. Это требование меняет методы getPinA и getPinB (см. листинг 14). Если входная линия ни к чему не подсоединена (None), то, как и раньше, будет задаваться вопрос пользователю. Однако, если она связана, то подключение осуществится, затребовав значение выхода fromgate. В свою очередь, это запускает логическую обработку вентилем поступивших данных. Процесс продолжается, пока есть доступные входы, и окончательное выходное значение становится требуемым входом для вентиля в вопросе. В каком-то смысле, схема работает в обратную сторону, чтобы найти входные данные, необходимые для производства конечного результата.

Листинг 14

def getPinA(self):
    if self.pinA == None:
        return input("Enter Pin A input for gate " + self.getName()+"-->")
    else:
        return self.pinA.getFrom().getOutput()

Следующий фрагмент конструирует схему, ранее показанную в этом разделе:

>>> g1 = AndGate("G1")
>>> g2 = AndGate("G2")
>>> g3 = OrGate("G3")
>>> g4 = NotGate("G4")
>>> c1 = Connector(g1,g3)
>>> c2 = Connector(g2,g3)
>>> c3 = Connector(g3,g4)

Выходы двух вентилей “И” (g1 и g2) соединены с вентилем “ИЛИ” (g3), а его выход - с вентилем “НЕ” (g4). Выход вентиля “НЕ” - это выход схемы целиком. Пример работы:

>>> g4.getOutput()
Pin A input for gate G1-->0
Pin B input for gate G1-->1
Pin A input for gate G2-->1
Pin B input for gate G2-->1
0

Попробуйте сами, используя ActiveCode 14.