Треугольник Серпинского¶

Ещё один фрактал, обладающий свойством самоподобия, - это треугольник Серпинского. Его пример показан на рисунке 3. Треугольник Серпинского иллюстрирует трёхходовой рекурсивный алгоритм. Процедура его отрисовки вручную очень проста. Начинаем с большого треугольника, который делим на четыре маленьких, связанных с серединами сторон первоначального. Игнорируя вновь созданный внутренний треугольник, делаем всё то же самое для каждого из трёх угловых. Каждый раз при создании нового набора треугольников, вы рекурсивно применяете эту процедуру к трём меньшим угловым фигурам. Так можно продолжать до бесконечности (если у вас достаточно острый карандаш). Перед тем, как продолжить чтение, можете попробовать самостоятельно нарисовать треугольник Серпинского, используя описанный метод.

Рисунок 3: Треугольник Серпинского.

Поскольку мы можем повторять этот алгоритм до бесконечности, что сделать базовым случаем? Им станет произвольное число - сколько раз мы хотим разделить треугольник на части. Иногда это число называют “степенью” фрактала. Каждый раз при рекурсивном вызове мы вычитаем из степени единицу, пока она не станет равной нулю. Тогда мы останавливаем рекурсию. Код, генерирующий треугольник Серпинского с рисунка 3, показан в ActiveCode 4.

Программа из ActiveCode 4 следует изложенным выше идеям. Первое, что делает sierpinski, - это прорисовывает внешний треугольник. Затем идут три рекурсивных вызова, по одному для каждого из новых угловых треугольников, полученных после соединения средних точек сторон. Мы снова используем стандартный модуль Python turtle. Вы можете изучить в подробностях все его методы, воспользовавшись командой help('turtle') в командной строке Python.

Посмотрите на код и подумайте, в каком порядке будут прорисовываться треугольники. Поскольку точный порядок углов определяется спецификацией начального набора, давайте предположим, что углы идут в следующем порядке: нижний левый, верхний, нижний правый. Так как функция sierpinski вызывает сама себя, вычисление будет идти к наименьшему возможному треугольнику в левом нижнем углу, а затем уже будут заполняться остальные треугольники в обратном порядке. Потом заполнятся треугольники в верхнем углу - к наименьшему и самому верхнему. Наконец, будут заполнен правый нижний угол, опять же по направлению к наименьшему нижнему правому.

Иногда полезно думать о рекурсивных алгоритмах в терминах диаграммы вызовов функции. Рисунок 4 показывает, что рекурсивные вызовы всегда начинаются слева. Активная функция выделена чёрным, неактивные вызовы - серым. Чем ниже вы спускаетесь по рисунку 4, тем меньше треугольники. Функция заканчивает рисунок одного уровня за один раз; закончив с нижней левой частью, она перемещается к нижней середине и так далее.

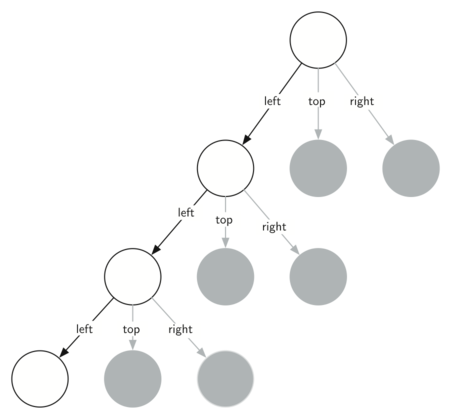
Рисунок 4: Построение треугольника Серпинского.

Функция sierpinski сильно зависит от функции getMid. Последняя принимает в качестве аргументов две конечные точки и возвращает точку, находящуюся по середине между ними. В дополнение, ActiveCode 4 содержит функцию раскраски треугольников, использующую методы begin_fill и end_fill из модуля turtle. Это означает, что каждая степень треугольника Серпинского рисуется другим цветом.