Сортировка слиянием¶

Теперь обратим наше внимание на использование стратегии “разделяй и властвуй”, как способа улучшить производительность сортировочных алгоритмов. Первым из них станет сортировка слиянием. Это рекурсивный алгоритм, который постоянно разбивает список пополам. Если список пуст или состоит из одного элемента, то он отсортирован по определению (базовый случай). Если в списке больше, чем один элемент, мы разбиваем его и рекурсивно вызываем сортировку слиянием для каждой из половин. После того, как обе они уже отсортированы, выполняется основная операция, называемая слиянием. Слияние - это процесс комбинирования двух меньших сортированных списков в один новый, но тоже отсортированный. Рисунок 10 демонстрирует в качестве примера наш старый знакомый список, который начинают разбивать с помощью mergeSort. Рисунок 11 показывает отсортированные списки и их слияние вместе.

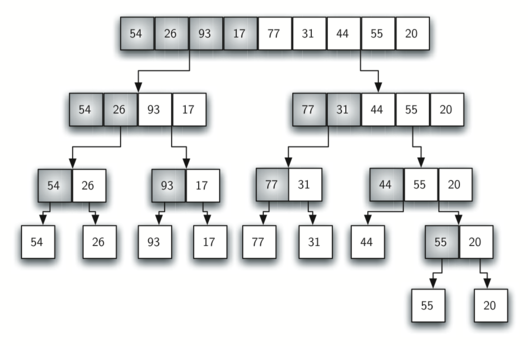
Рисунок 10: Разбиение списка в сортировке слиянием

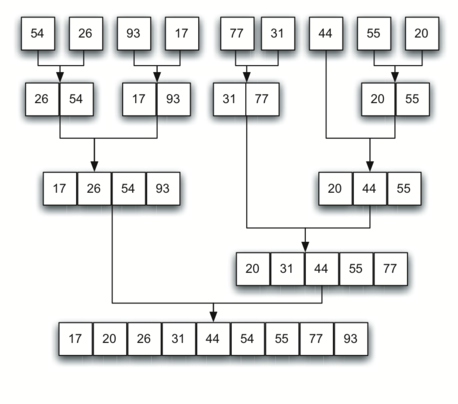
Рисунок 11: Списки, которые соединяются вместе

Функция mergeSort, показанная в ActiveCode 6, начинает с проверки базового условия. Если длина списка меньше или равна единице, то он уже отсортирован, и в дальшейшей обработке нет необходимости. С другой стороны, если длина больше единицы, то мы используем операцию Python slice, чтобы извлечь правую и левую части. Важно отметить, что список может иметь нечётное количество элементов. Для алгоритма это не принципиально, поскольку длины будут различаться максимум на единицу.

После того, как функция mergeSort была вызывана для правой и левой частей (строки 8 - 9), предполагается, что они отсортированы. Остаток функции (строки 11 - 31) отвечает за слияние двух меньших сортированных списков в больший. Обратите внимание, что операция слияния помещает элементы обратно в оригинальный список (alist) по одному за раз с помощью повторяющегося выбора наименьшего элемента из двух сортированных списков.

Функцию mergeSort дополняет оператор print (строка 2), который выводит содержимое сортируемого списка на начало каждого вызова. Также есть оператор print (строка 32), показывающий процесс слияния. Результат вычисления функции в нашем примере списка выводится на экран. Обратите внимание, что список с 44, 55 и 20 не делится поровну. Первая его часть равна [44], а вторая - [55, 20]. Легко увидеть, как процесс разбивки в итоге приводит к тому, что список может быть немедленно слит с другими сортированными списками.

Для большей детализации, CodeLens позволят вам пошагово пройти весь алгоритм.

Чтобы проанализировать функцию megreSort, нам надо рассмотреть два различных процесса, которые в ней происходят. Во-первых, список разбивается пополам. Мы уже вычисляли (для бинарного поиска), что разделять список на две половины можно \(\log n\) раз, где \(n\) - длина списка. Второй процесс - это слияние. Каждый элемент будет обработан и помещён в сортированный список. Таким образом, операция слияния, чей результат - список из \(n\) элементов, потребует \(n\) операций. Итог данного анализа: \(\log n\) разбиений, каждое стоимостью \(n\), что в сумме даст \(n\log n\) операций. Таким образом, сортировка слиянием - \(O(n\log n)\) алгоритм.

Напомним, что встроенный оператор разбиения имеет \(O(k)\), где k - размер разбиения. Чтобы гарантировать для сортировки слиянием \(O(n\log n)\), нам нужно от него избавиться. Напомним, что это возможно, если просто помещать начальный и конечный индексы вместе со списком в качестве аргументов рекурсивного вызова. Мы оставляем это вам в качестве упражнения.

Важно отметить, что функция mergeSort требует дополнительного места для хранения двух извлечённых операцией разбиения частей. Это дополнительное пространство может стать критичным фактором, если список велик, и сделать этот способ сортировки проблемным для больших наборов данных.