Производительность АВЛ-дерева¶

Прежде, чем идти дальше, давайте рассмотрим результат соблюдения этого нового фактора баланса. Утверждением для доказательства станет гарантия, что если дерево имеет фактор сбалансированности -1, 0 или 1, то мы получаем лучшую О-производительность для операций с ключами. Начнём с размышлений о том, как условие баланса изменяет наихудший случай. Есть две возможности, которые следует рассмотреть: перевес дерева влево и вправо. Мы будем изучать деревья высотой 0, 1, 2, и 3, и рисунок 2 иллюстрирует дерево максимально перевешивающее влево согласно новым правилам.

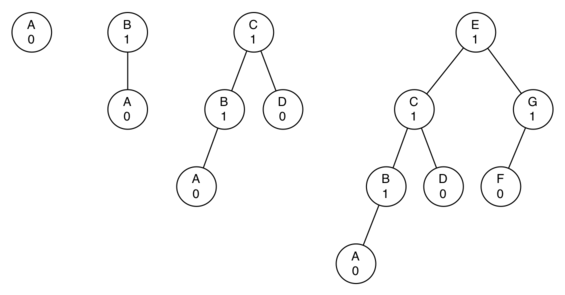
Рисунок 2: Худший случай перевешивающих влево АВЛ-деревьев.

Глядя на общее количество узлов, можно заметить, что для дерева высотой 0 оно равно 1, высотой 1 - $1+1 = 2$ , высотой 2 - $1+1+2 = 4$ , высотой 3 - $1 + 2 + 4 = 7$ . Обобщая, количество узлов для дерева высотой $h$ ( $N_h$ ) равно

$N_h = 1 + N_{h-1} + N_{h-2}$

Эта рекуррентность может показаться вам знакомой, поскольку очень похожа на последовательность Фибоначчи. Данный факт можно использовать для вывода формулы высоты АВЛ-дерева с заданным количеством узлов. Напомним, что в последовательности Фибоначчи $i_{ое}$ число равно

$\begin{split}F_0 = 0 \\ F_1 = 1 \\ F_i = F_{i-1} + F_{i-2} \text{ for all } i \ge 2\end{split}$

Важный математический результат заключается в том, что числа Фибоначчи с каждым разом становятся всё больше и больше, а отношение $F_i / F_{i-1}$ всё ближе и ближе к “золотому сечению” $\Phi$ , определяемому как $\Phi = \frac{1 + \sqrt{5}}{2}$ . Вы можете обратиться к текстам по математике, если хотите посмотреть вывод предыдущего уравнения. Мы же просто используем его для приближённого вычисления $F_i$ как $F_i = \Phi^i/\sqrt{5}$ . Если переписать уравнение для $N_h$ с использованием этой аппроксимации, то получится

$N_h = F_{h+2} - 1, h \ge 1$

Заменив ссылку на Фибоначчи его аппроксимацией к “золотому сечению”, получим

$N_h = \frac{\Phi^{h+2}}{\sqrt{5}} - 1$

Перегруппировав переменные и взяв от обоих частей логарифм по основанию 2, получим следующее решение:

$\begin{split}\log{N_h+1} = (H+2)\log{\Phi} - \frac{1}{2} \log{5} \\ h = \frac{\log{N_h+1} - 2 \log{\Phi} + \frac{1}{2} \log{5}}{\log{\Phi}} \\ h = 1.44 \log{N_h}\end{split}$

Это выражение говорит о том, что каждый раз высота АВЛ-дерева равна константе (1.44), умноженной на логарифм высоты дерева. И это отличная новость для поиска по АВЛ-дереву, поскольку ограничивает его $O(\log{N})$ .

Next Section - Реализация АВЛ-дерева