Реализация двоичной кучи¶

Структурное свойство¶

Чтобы сделать работу нашей реализации кучи более эффективной, воспользуемся преимуществами логарифмической природы представляющего её двоичного дерева. Для гарантии логарифмической производительности нам необходимо поддерживать дерево сбалансированным. Сбалансированное двоичное дерево имеет примерно одинаковое количество узлов в своих правых и левых поддеревьях. В нашей реализации баланс будет поддерживаться созданием полного двоичного дерева, у которого каждый уровень (кроме последнего) целиком заполнен. Самый же нижний уровень заполняется слева направо. Полное двоичное дерево показано на рисунке 1.

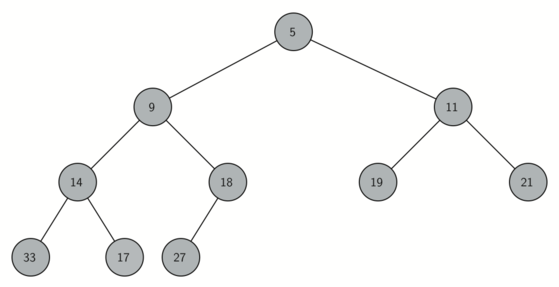
Рисунок 1: Полное двоичное дерево

Другим любопытным свойством такого дерева является то, что мы можем представить его, используя обычный список. Нет нужды в применении узлов и ссылок или списка списков. Поскольку дерево полное, то левым потомком родителя (позиция \(p\)) будет узел, расположенный на позиции \(2p\) в списке. Аналогично, правый потомок находится на позиции \(2p + 1\). Чтобы найти предка любого узла, достаточно просто использовать целочисленное деление. Если индекс узла - \(n\), то его родитель будет иметь \(n/2\). Рисунок 2 демонстрирует полное двоичное дерево, а также приводит его списковое представление. Отметьте отношения \(2p\) и \(2p+1\) между родителями и потомками. Списковое представление дерева совместно со свойством полноты структуры позволяет нам эффективно обходить двоичные деревья, используя всего несколько простых математических операций. Мы увидим, что это также влечёт за собой эффективную реализацию нашей двоичной кучи.

Свойство упорядоченности кучи¶

Способ, который мы используем для хранения элементов в куче, зависит от поддержки ею свойства упорядоченности. Свойство упорядоченности кучи заключается в следующем: для каждого узла \(x\) и его родителя \(p\) ключ \(p\) меньше или равен ключу \(x\). Полное двоичное дерево, показанное на рисунке 2, также обладает этим свойством.

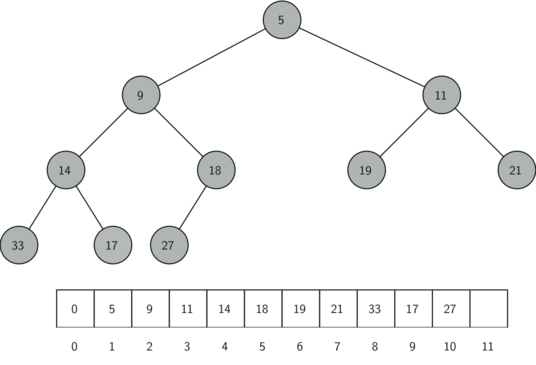
Рисунок 2: Полное двоичное дерево и его списковое представление.

Операции с кучей¶

Начнём воплощение нашего двоичного дерева с конструктора. Поскольку оно целиком может быть представлено в виде обычного списка, то всё, что ему нужно делать, - это инициализировать список и атрибут currentSize, через который отслеживается текущий размер кучи. Код конструктора показан в листинге 1. Вы можете заметить, что пустая двоичная куча содержит нуль, как первый элемент heapList. Он не используется, но необходим для целочисленного деления, применяемого в последующих методах.

Листинг 1

class BinHeap:
    def __init__(self):
        self.heapList = [0]
        self.currentSize = 0

Следующим будет метод insert. Простейший и наиболее эффективный способ добавить элемент - просто присоединить его к концу списка. Хорошей новостью станет то, что таким образом мы поддержим свойство полноты дерева. Плохой - весьма вероятно, что это нарушит структурное свойство кучи. Однако, существует способ написать метод, позволяющий нам восстановить структуру с помощью сравнения нового элемента с его предком. Если добавляемый элемент меньше родителя, то мы можем просто поменять их местами. Рисунок 2 показывает серию перестановок, необходимую для “просачивания” нового элемента на его законное место в дереве.

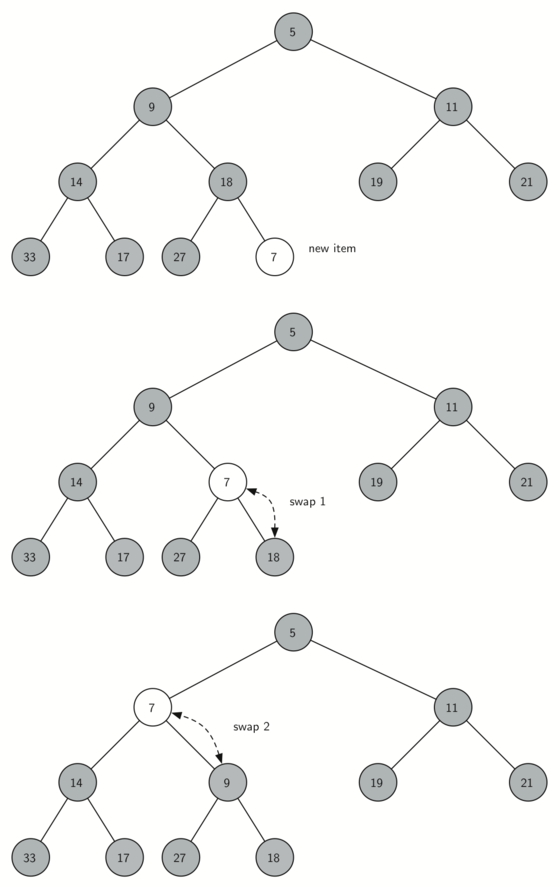
Рисунок 2: “Просачивание” нового элемента на его правильную позицию.

Обратите внимание, при прохождении элемента вверх, мы восстанавливаем свойство кучи между новым элементом и его родителем. Так же это свойство сохраняется для всех его братьев. Конечно, если элемент достаточно мал, нам всё ещё может понадобиться передвинуть его на уровень выше. Фактически, мы можем перемещать элемент до самого верха дерева. Листинг 2 демонстрирует метод percUp, поднимающий новый элемент настолько высоко, насколько это требуется для поддержки свойства кучи. Вот где важен наш лишний элемент в heapList. Заметьте, мы можем рассчитать позицию родителя любого узла с помощью обычного целочисленного деления (делением его индекса на два).

Теперь мы готовы написать метод insert (см. листинг 3). Большую часть его работы уже делает percUp. После того, как в дерево вставлен новый элемент, percUp позиционирует его как положено.

Листинг 2

def percUp(self,i):
    while i // 2 > 0:
      if self.heapList[i] < self.heapList[i // 2]:
         tmp = self.heapList[i // 2]
         self.heapList[i // 2] = self.heapList[i]
         self.heapList[i] = tmp
      i = i // 2

Листинг 3

def insert(self,k):
    self.heapList.append(k)
    self.currentSize = self.currentSize + 1
    self.percUp(self.currentSize)

С правильно определённым методом insert мы можем перейти к методу delMin. Так как свойство кучи требует, чтобы корень был наименьшим элементом дерева, найти её минимум очень легко. Сложная часть delMin - восстановить соответствие свойствам структуры и упорядоченности кучи после удаления корневого элемента. Мы будем это делать в два шага. Во-первых, восстановим корневой элемент, взяв последний элемент списка и передвинув его на место корня. Так мы поддержим структурное свойство кучи. Однако, весьма вероятно, что при этом нарушится её свойство упорядоченности. Поэтому вторым шагом станет спуск корня на его правильную позицию. На рисунке 3 показана серия перестановок, необходимая для перемещения корня до соответствующего положения в куче.

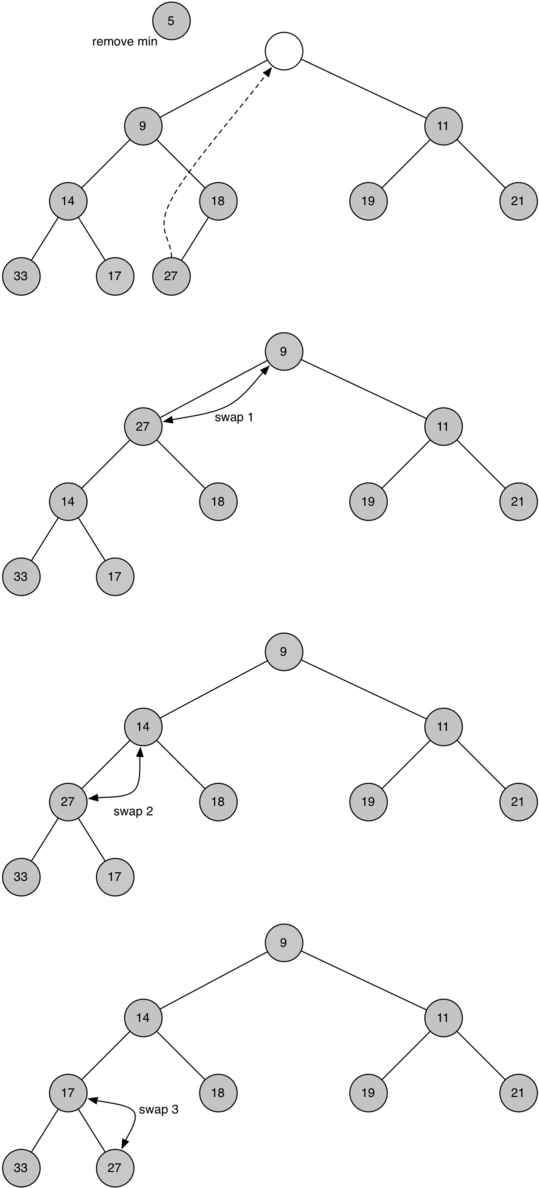
Рисунок 3: “Просачивание” корневого узла вниз по дереву.

Чтобы поддержать свойство упорядоченности, нам надо всего лишь поменять местами корень с меньшим, чем он, потомком. После начальной перестановки мы можем повторять процесс для узла и его потомков до тех пор, пока он не переместится на позицию, в которой будет меньше обоих своих детей. Код для “просачивания” узла вниз по дереву можно найти в методах percDown и minChild из листинга 4.

Листинг 4

def percDown(self,i):
    while (i * 2) <= self.currentSize:
        mc = self.minChild(i)
        if self.heapList[i] > self.heapList[mc]:
            tmp = self.heapList[i]
            self.heapList[i] = self.heapList[mc]
            self.heapList[mc] = tmp
        i = mc

def minChild(self,i):
    if i * 2 + 1 > self.currentSize:
        return i * 2
    else:
        if self.heapList[i*2] < self.heapList[i*2+1]:
            return i * 2
        else:
            return i * 2 + 1

Код для операции delMin находится в листинге 5. Заметьте, вся сложная работа снова отдана вспомогательной функции (в данном случае - percDown).

Листинг 5

def delMin(self):
    retval = self.heapList[1]
    self.heapList[1] = self.heapList[self.currentSize]
    self.currentSize = self.currentSize - 1
    self.heapList.pop()
    self.percDown(1)
    return retval

Заканчивая дискуссию о двоичных деревьях, рассмотрим метод, позволяющий построить кучу из списка ключей. Первый способ, который мог прийти вам в голову, следующий. Имея список ключей, можно легко построить кучу, вставляя по ключу за раз. Поскольку вы начинаете со списком из одного элемента, то он отсортирован и можно использовать бинарный поиск для вычисления позиции, куда вставлять следующий ключ (это будет стоить примерно \(O(\log{n})\). Однако, вспомните: вставка элемента в середину может потребовать \(O(n)\) операций сдвига остатка списка, чтобы освободить место новому ключу. Таким образом, вставка в кучу из \(n\) ключей в общем потребует \(O(n \log{n})\) операций. А если мы начнём со списка целиком, то кучу можно будет построить за \(O(n)\) операций. Листинг 6 демонстрирует, как это можно сделать.

Листинг 6

def buildHeap(self,alist):
    i = len(alist) // 2
    self.currentSize = len(alist)
    self.heapList = [0] + alist[:]
    while (i > 0):
        self.percDown(i)
        i = i - 1

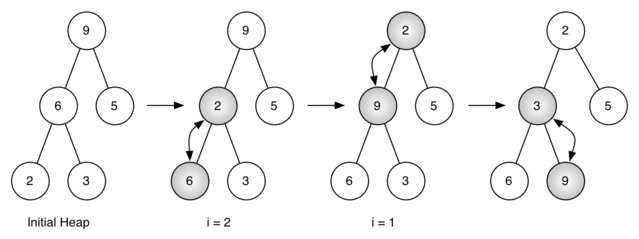
Рисунок 4: Создание кучи из списка [9, 6, 5, 2, 3]

Рисунок 4 показывает перестановки, которые делает метод buildHeap, перемещая узлы начального дерева [9, 6, 5, 2, 3] на их правильные позиции. Хотя мы начинаем с середины дерева и работаем в обратном от корня направлении, метод percDown гарантирует, что наибольший элемент всегда спустится вниз по дереву. Поскольку куча - полное двоичное дерево, любой прошедший половину пути узел будет листом и, следовательно, не иметь потомков. Обратите внимание: при i=1 мы просачиваемся вниз от корня дерева, т.е. это может потребовать несколько обменов. Как вы можете видеть, в самом правом из двух деревьев на рисунке 4 первая 9 перемещается из корневой позиции, но после того, как она опустится на уровень вниз, percDown гарантирует проверку следующего набора потомков ниже по дереву на то, что их предок стоит настолько низко, насколько это возможно. В данном случае результатом станет второй обмен с 3. Теперь 9 спущено на самый нижний уровень дерева, и больше нельзя сделать никаких обменов. Полезно сравнить списковое представление показанной на рисунке 4 серии обменов с представлением в виде дерева.

i = 2  [0, 9, 5, 6, 2, 3]
i = 1  [0, 9, 2, 6, 5, 3]
i = 0  [0, 2, 3, 6, 5, 9]

Полностью реализация двоичной кучи показана в ActiveCode 2.

Утверждение, что мы можем построить кучу за \(O(n)\) сначала может показаться немного таинственным, и доказательство его выходит за пределы обсуждения в этой книге. Однако, ключом к пониманию может стать напоминание о \(\log{n}\) факторе, выводимом из высоты дерева. Для большей части работы в buildHeap дерево короче, чем \(\log{n}\).

Используя тот факт, что кучу из списка можно создать за \(O(n)\) времени, в конце этой главы вы получите в качестве упражнения задание сконструировать использующий кучу алгоритм, который сортирует список за \(O(n\log{n}))\).