Вопросы для обсуждения¶

1. Нарисуйте дерево, которое будет результатом следующего перечня вызовов функций:

>>> r = BinaryTree(3)
>>> insertLeft(r,4)
[3, [4, [], []], []]
>>> insertLeft(r,5)
[3, [5, [4, [], []], []], []]
>>> insertRight(r,6)
[3, [5, [4, [], []], []], [6, [], []]]
>>> insertRight(r,7)
[3, [5, [4, [], []], []], [7, [], [6, [], []]]]
>>> setRootVal(r,9)
>>> insertLeft(r,11)
[9, [11, [5, [4, [], []], []], []], [7, [], [6, [], []]]]

1. Сделайте трассировку алгоритма для создания дерева из выражения \((4 * 8) / 6 - 3\).
2. Рассмотрим следующий список целых чисел: [1,2,3,4,5,6,7,8,9,10]. Покажите двоичное дерево поиска, получающееся в результате вставки чисел в список.
3. Рассмотрим следующий список целых чисел: [10,9,8,7,6,5,4,3,2,1]. Покажите двоичное дерево поиска, получающееся в результате вставки чисел в список.
4. Сгенерируйте список из случайных целых чисел. Покажите двоичное дерево кучи, получающееся в результате их вставки в список по одному.
5. Используя список из предыдущего вопроса, покажите двоичное дерево кучи, получающееся в результате его использования в качестве параметра метода buildHeap. Продемонстрируйте обе формы: в виде списка и в виде дерева.
6. Нарисуйте двоичное дерево поиска, которое будет результатом вставки следующих ключей в заданном порядке: 68, 88, 61, 89, 94, 50, 4, 76, 66 и 82.
7. Сгенерируйте список случайных целых чисел. Нарисуйте двоичное дерево поиска, получающееся в результате их вставки в список.
8. Рассмотрим следующий список: [1,2,3,4,5,6,7,8,9,10]. Покажите двоичную кучу, которая будет результатом вставки чисел по одному за раз.
9. Рассмотрим следующий список: [10,9,8,7,6,5,4,3,2,1]. Покажите двоичную кучу, которая будет результатом вставки чисел по одному за раз.
10. Рассмотрите две различные техники, которые мы использовали для реализации проходов по двоичному дереву. Почему мы делаем проверку перед вызовом preorder, когда реализуем метод, хотя для функции она происходит внутри вызова?
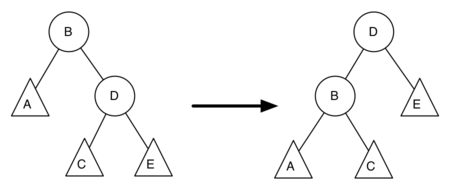
11. Покажите функциональные вызовы, необходимые для построения следующего двоичного дерева:

1. Выполните соответствующие вращения для заданного дерева, чтобы привести его в сбалансированное состояние.

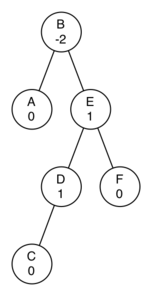
1. Используя следующий рисунок, как стартовую точку, выведите уравнение, дающее обновление фактора сбалансированности для узла D.