Анализ деревьев поиска¶

Имея полную реализацию двоичного дерева поиска, давайте быстро проанализируем написанные для неё функции. Начнём с метода put. Ограничивающим фактором его производительности является высота двоичного дерева. Напомним определение из раздела о терминологии: высота дерева - это количество ветвей между корнем и наиболее глубоко расположенным листом. Она будет ограничивающим фактором, потому что, когда мы ищем подходящее место для вставки узла, на каждом уровне требуется как минимум одно сравнение.

Но какова вероятная высота двоичного дерева? Ответ на этот вопрос зависит от того, как в него добавлялись ключи. Если это происходило в произвольном порядке, то высота будет примерно \(\log_2{n}\), где \(n\) - количество узлов в дереве. Это происходит от того, что при случайном распределении ключей около половины из них окажется меньше корня, а остальные - больше. Вспомните: двоичное дерево имеет один корень, потом уровень с двумя узлами, потом с четыремя и так далее. Количество узлов на каждом конкретном уровне - \(2^d\), где \(d\) - его глубина. Общее число узлов в идеально сбалансированном двоичном дереве равно \(2^{h+1}-1\), где \(h\) представляет собой высоту дерева.

Идеально сбалансированное дерево имеет одинаковое количество узлов в левом и правом поддеревьях. Для него производительность put в наихудшем случае будет \(O(\log_2{n})\), где \(n\) - общее количество узлов. Отметьте обратное отношение вычислений по сравнению с предыдущим абзацем. Итак, \(\log_2{n}\) даст нам высоту дерева и максимальное число сравнений, которое потребуется put, чтобы найти подходящее место для вставки нового узла.

К сожалению, остаётся вероятность сконструировать дерево поиска с высотой, равной \(n\). Это случится, если вставлять ключи в отсортированном порядке. Пример такого дерева приведён на рисунке 6. В этом случае производительность метода put равна \(O(n)\).

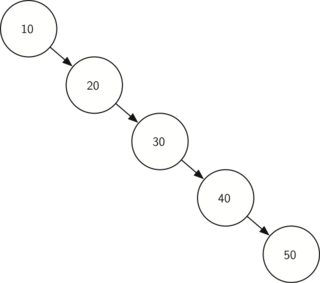
Рисунок 6: Перекошенное двоичное дерево будет иметь низкую производительность.

После того, как мы разобрались, что производительность метода put ограничена высотой дерева, возможно, вы сумеете догадатьсяоб ограничениях остальных методов - get, in, и del. Поскольку get ищет в дереве ключ, то в наихудшем случае искомое окажется в самом низу. На первый взгляд случай del кажется более сложным, поскольку здесь требуется искать преемника для проведения операции удаления. Но вспомните: ограничение для его поиска при наихудшим сценарии - тоже высота дерева, что означает простое дублирование работы. Это константный фактор, так что он не меняет наихудший случай.