Реализация упорядоченного списка¶

Перед тем, как начать реализовывать упорядоченный список, мы должны вспомнить, что положение элементов относительно друг друга основываются на некой базовой характеристике. Упорядоченный список целых чисел, представленный выше (17, 26, 31, 77 и 93), может быть выражен связанной структурой, показанной на Рисунке 15. Опять же, узел и ссылка идеально подходят для представления взаимного расположения элементов.

Рисунок 15: Упорядоченный связанный список

Для реализации класса OrderedList мы будем использовать ту же технику, что и для неупорядоченного списка. Пустой список вновь будет обозначаться ссылкой head на None (см. Листинг 8).

Листинг 8

class OrderedList:
    def __init__(self):
        self.head = None

Рассматривая операции для упорядоченного списка, стоит отметить, что методы isEmpty и size могут быть реализованы аналогично неупорядоченному списку, поскольку имеют дело только с количеством узлов безотносительно их содержимого. Также хорошо будет работать метод remove, потому что нам по-прежнему надо искать элемент, а затем окружающие узел ссылки, чтобы удалить его. Два оставшихся метода - search и add - потребуют некоторой модификации.

Поиск в неупорядоченном списке требует, чтобы мы обходили узлы по одному за раз, пока не найдём искомый элемент или не выйдем за пределы списка (None). Такой подход будет работать и для упорядоченного списка. В том случае, когда элемент найдётся, - он будет тем, что нам нужен. Однако, в случае, когда элемент не содержится в списке, мы можем воспользоваться преимуществом упорядочения, чтобы остановить поиск как можно раньше.

Например, Рисунок 16 показывает упорядоченный связанный список, в котором ищется значение 45. В процессе обхода мы начинаем с головы списка и сначала проверяем на соответствие 17. Поскольку 17 - не то, что мы ищем, то смещаемся к следующему узлу - 26. Это снова не то, и мы перемещаемся к 31, а затем к 54. В этот момент кое-что изменилось. Поскольку 54 не тот элемент, что мы ищем, наша предыдущая стратегия должна заключаться в продвижении вперёд. Однако, с учётом того факта, что список упорядочен, в этом больше нет необходимости. Раз значение в узле больше, чем искомое, значит поиск можно останавливать и возвращать False. Не существует способа значению оказаться среди остатка упорядоченного списка.

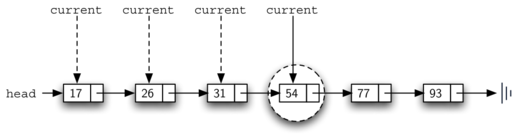
Рисунок 16: Поиск в упорядоченном списке

Листинг 9 показывает законченный метод search. Новое условие, обсуждаемое выше, можно вставить очень легко: добавить ещё одну булеву переменную - stop - и инициализировать её False (строка 4). Пока stop равно `False` мы можем продолжать поиск в списке (строка 5). Если в любом из узлов обнаружится значение больше искомого, то мы установим stop в True (строки 9-10). Оставшиеся строки идентичны поиску в неупорядоченном списке.

Листинг 9

def search(self,item):
    current = self.head
    found = False
    stop = False
    while current != None and not found and not stop:
        if current.getData() == item:
            found = True
        else:
            if current.getData() > item:
                stop = True
            else:
                current = current.getNext()

    return found

Наиболее значительная модификация затронет метод add. Напомним, что в неупорядоченных списках он просто помещал новый элемент в голову списка - самую доступную точку. К сожалению, с упорядоченным списком это больше не сработает. Теперь нам надо искать специальное место, где будет размещаться новый элемент среди уже существующих в упорядоченном списке.

Предположим, что у нас есть упорядоченный список из 17, 26, 54, 77 и 93, и мы хотим добавить в него значение 31. Метод add должен решить, что новый элемент следует расположить между 26 и 54. Рисунок 17 показывает необходимую вставку. Как мы объясняли ранее, нам нужно обойти связанный список в поисках места, куда будет вставлен новый элемент. Мы знаем, что место найдено, если мы или вышли за пределы списка (current равно None), или значение текущего узла стало больше, чем добавляемый элемент. В нашем примере нас вынудит остановится появление значения 54.

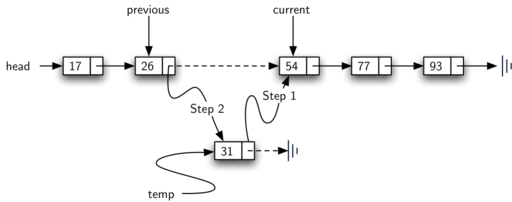
Рисунок 17: Добавление элемента в упорядоченный связанный список

Как мы уже видели для неупорядоченных списков, здесь понадобится дополнительная ссылка (previous), поскольку current не сможет предоставить доступ к узлу, который нужно будет изменить. Листинг 10 показывает законченный метод add. Строки 2-3 устанавливают две внешние ссылки, а строки 9-10 вновь позволяют previous следовать на один узел после current во время каждой итерации. Условие в строке 5 разрешает итерациям продолжаться до тех пор, пока остаются непросмотренные узлы и значение текущего не превышает искомое. Противный случай - когда итерация терпит неудачу - означает, что мы нашли место для нового узла.

Остаток метода завершает двухшаговый процесс, показанный на Рисунке 17. Поскольку для элемента был создан новый узел, то остаётся единственный вопрос: куда он будет добавлен - в начало или в середину связанного списка? Для ответа на него вновь используется previous == None.

Листинг 10

def add(self,item):
    current = self.head
    previous = None
    stop = False
    while current != None and not stop:
        if current.getData() > item:
            stop = True
        else:
            previous = current
            current = current.getNext()

    temp = Node(item)
    if previous == None:
        temp.setNext(self.head)
        self.head = temp
    else:
        temp.setNext(current)
        previous.setNext(temp)

Класс `OrderedList` с реализованными на данный момент методами можно найти в ActiveCode 4.

Оставшиеся операции мы оставляем в качестве упражнения. Вам следует внимательно рассмотреть, когда неупорядоченная реализация будет работать как следует с учётом того, что теперь список упорядочен.