Алгоритм Дейкстры¶

Для поиска кратчайшего пути мы собираемся использовать так называемый “алгоритм Дейкстры”. Он является итеративным и возвращает кратчайшее расстояние от конкретного стартового узла до всех прочих узлов графа - результат, снова похожий на поиск в ширину.

Чтобы отслеживать общие затраты на продвижение от начального узла до каждого конечного пункта, мы используем поле dist класса Vertex. Оно будет содержать текущий общий вес кратчайшего пути от старта до запрашиваемой вершины. Алгоритм повторяется для каждого узла в графе, однако, последовательность итераций задаётся очередью с приоритетом. Значение, используемое для определения порядка объектов в ней, - dist. Когда вершина только создаётся, dist устанавливается в очень большую величину. Теоретически ею должна быть бесконечность, но на практике мы просто выбираем число, большее любого реального расстояния, которое будет использоваться при решении задачи.

Код алгоритма Дейкстры показан в листинге 1. Результатом его работы станут правильно установленные расстояния, а также ссылки на предшественника для каждой вершины графа.

Листинг 1

from pythonds.graphs import PriorityQueue, Graph, Vertex
def dijkstra(aGraph,start):
    pq = PriorityQueue()
    start.setDistance(0)
    pq.buildHeap([(v.getDistance(),v) for v in aGraph])
    while not pq.isEmpty():
        currentVert = pq.delMin()
        for nextVert in currentVert.getConnections():
            newDist = currentVert.getDistance() \
                    + currentVert.getWeight(nextVert)
            if newDist < nextVert.getDistance():
                nextVert.setDistance( newDist )
                nextVert.setPred(currentVert)
                pq.decreaseKey(nextVert,newDist)

Алгоритм Дейкстры использует очередь с приоритетом. Вы можете помнить, что она основывается на куче, которую мы реализовали в главе, посвящённой деревьям. Однако, между тем простым вариантом и реализацией для алгоритма Дейкстры есть несколько отличий. Во-первых, класс PriorityQueue сохраняет кортежи пар ключ-значение. Это очень важно для алгоритма Дейкстры, поскольку ключи в очереди с приоритетом должны быть связаны с ключами вершин графа. Во-вторых, значение используется для определения приоритета, а следовательно - для определения позиции ключа в очереди. В этой реализации мы используем растояние до вершины как приоритет, покольку (как увидим дальше) для исследования мы всегда будем стремиться найти узел с наименьшим расстоянием. Следующее отличие - в дополнительном методе decreaseKey. Как вы можете видеть, он используется, когда нужно уменьшить расстояние до вершины, уже находящейся в очереди, т.е. переместить её ближе к началу.

Давайте пройдём по алгоритму Дейкстры для одного из узлов, используя в качестве путеводителя нижеследующие рисунки. Начнём с вершины \(u\). С нею смежны три узла: \(v, w\) и \(x\). Поскольку начальные расстояния для них инициализированы sys.maxint, то расстояниями пути к ним от стартового узла станут их непосредственные веса. Вместе с обновлением издержек мы устанавливаем предшественником каждого узел \(u\) и добавляем их в очередь. Расстояние будет использоваться как ключ приоритета. Состояние алгоритма на этот момент показано на рисунке 3.

На следующей итерации цикла while мы проверяем вершины, смежные с \(x\). Она выбрана следующей, поскольку имеет наименьшее значение dist и, следовательно, оказалась наверху очереди с приоритетом. Для \(x\) мы рассматриваем её соседей \(u, v, w\) и \(y\). Для каждого из них расчитываем путь через \(x\) и смотрим, у кого он будет меньше существующей величины dist. Очевидно, что это вариант \(y\), поскольку его расстояние - sys.maxint, а не \(u\) или \(v\), поскольку их значения 0 и 2 соответственно. Как бы то ни было, теперь мы знаем, что расстояние до \(w\) будет наименьшим, если идти к ней через \(x\), а не непосредственно от \(u\) к \(w\). Таким образом, мы обновляем расстояние \(w\) и изменяем её предшественника с \(u\) на \(x\). См. рисунок 4, где показано состояние всех вершин на данный момент.

Следующим шагом станет рассмотрение соседей \(v\) (см. рисунок 5). Результаты этого шага не изменят граф, так что мы переходим к узлу \(y\). Для него (см. рисунок 6) мы находим, что дешевле пройти через \(w\) и \(z\), в связи с чем регулируем соответствующие расстояния и ссылки на предшественников. Наконец, проверяем узлы \(w\) и \(z\) (см. рисунок 7 и рисунок 8). Однако, никаких дополнительных изменений это не вносит, очередь с приоритетом пуста и алгоритм Дейкстры заканчивает свою работу.

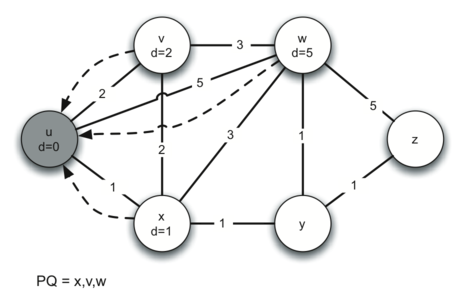
Рисунок 3: Трассировка алгоритма Дейкстры

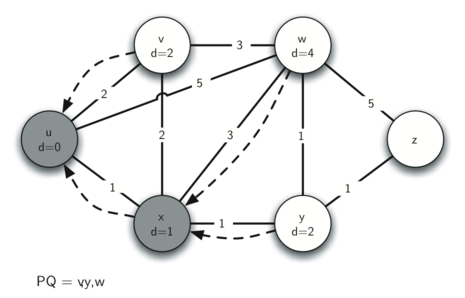
Рисунок 4: Трассировка алгоритма Дейкстры

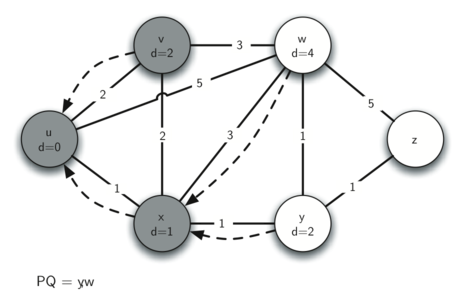
Рисунок 5: Трассировка алгоритма Дейкстры

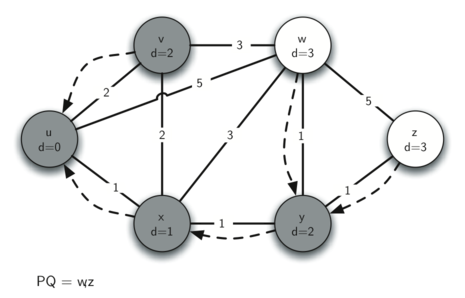
Рисунок 6: Трассировка алгоритма Дейкстры

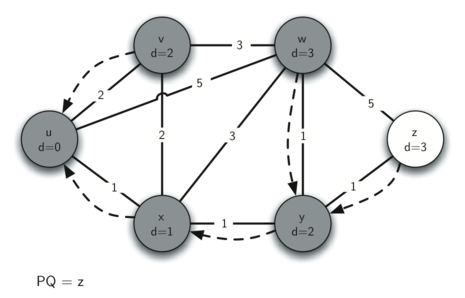
Рисунок 7: Трассировка алгоритма Дейкстры

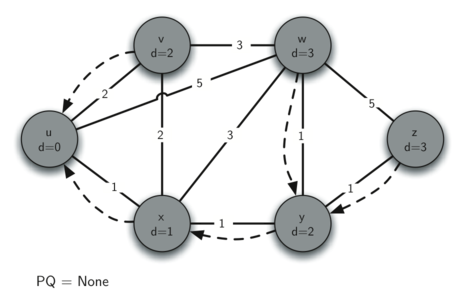
Рисунок 8: Трассировка алгоритма Дейкстры

Важно отметить, что алгоритм Дейкстры работает только в том случае, когда веса рёбер положительны. Вы можете самостоятельно проверить, что если хотя бы у одного из них будет отрицательный вес, то алгоритм никогда не завершится.

Отметим, что для прокладывания маршрута сообщения через интернет используются и другие алгоритмы поиска кратчайшего пути. Одной из проблем с алгоритмом Дейкстры для Всемирной паутины является необходимость иметь полное представление графа. Только в этом случае он может быть запущен. Следствием этого будет то, что каждый маршрутизатор должен обладать полной картой всех маршрутизаторов в интернете. На практике такое не встречается, поэтому существуют дргие варианты алгоритма, позволяющие маршрутизатору открывать граф по ходу дела. Одни из таких алгоритмов, о котором вы, возможно, захотите почитать, называется “дистанционно-векторный алгоритм маршрутизации”.