Реализация поиска в ширину¶
После создания графа мы можем переключиться на алгоритм, который будем использовать для поиска кратчайшего решения “словесной лестницы”. Этот алгоритм для графов называется “поиск в ширину”. Поиск в ширину (BFS - от англ. breadth first search) - один из самых лёгких алгоритмов поиска в графе. Так же он служит прототипом некоторых других важных алгоритмов, которые мы изучим позже.
Для заданных графа \(G\) и начальной вершины \(s\) работа поиска в ширину заключается в исследовании рёбер графа с целью найти все вершины \(G\), к которым существет путь из \(s\). Замечательной особенностью поиска в ширину является то, что он находит все вершины на расстоянии \(k\) от \(s\) до того, как начинает искать любую из вершин на расстоянии \(k+1\). Одним из хороших способов визуализации поиска в ширину будет представление о том, что он строит дерево, по одному уровню за раз. Алгоритм добавляет всех детей начальной вершины до того, как обнаруживает любого из её внуков.
Чтобы отслеживать своё продвижение, BFS окрашивает каждую вершину в белый, серый или чёрный цвета. Все вершины при создании инициализируются белым. Когда вершина обнаруживается в превый раз, то ей задаётся серый цвет. Когда же BFS её полностью исследует, вершина окрашивается в чёрный. Это означает, что не существует смежных с ней белых вершин. С другой стороны, серый узел может иметь несколько связанных с ним белых вершин, показывая, что у нас ещё есть пространство для исследования.
Алгоритм поиска в ширину показан ниже в листинге 2. Он использует представление графа в виде списка смежности, разработанное нами ранее. Дополнительно используется Queue - ключевой момент, как мы увидим, - чтобы решить, какую вершину исследовать следующей.
Так же алгоритм BFS использует расширенную версию класса Vertex. В неё добавлены три поля класса: расстояние, предшественник и цвет. Каждое из них также имеет соответствующие методы установки и считывания значения. Код расширенного класса Vertex включён в пакет pythonds, но мы покажем его здесь, чтобы было ясно, что там нет ничего нового для изучения, кроме дополнительных атрибутов.
BFS начинается с вершины s и окрашивает start в серый, показывая, что она изучается в настоящий момент. Два других значения - расстояние и предшественник - инициализируются 0 и None соответственно. Наконец, start помещается в Queue. Следующим шагом будет систематическое исследование вершин в начале очереди. Мы исследуем каждый новый узел, находящийся на этой позиции, путём перебора его списка смежности. Каждый из узлов списка будет проверен на цвет. Если он белый, то вершина неисследована, и произойдут следующие четыре вещи:
- Новая неисследованная вершина nbr окрашивается в серый.
- Предшественником nbr устанавливается текущий узел currentVert.
- Расстояние nbr устанавливается равным расстоянию currentVert + 1.
- nbr добавляется в конец очереди. Это эффективно планирует дальнейшее исследование этого узла, но не прежде, чем будут исследованы остальные вершины из списка смежности currentVert.
Листинг 2
from pythonds.graphs import Graph, Vertex
from pythonds.basic import Queue
def bfs(g,start):
start.setDistance(0)
start.setPred(None)
vertQueue = Queue()
vertQueue.enqueue(start)
while (vertQueue.size() > 0):
currentVert = vertQueue.dequeue()
for nbr in currentVert.getConnections():
if (nbr.getColor() == 'white'):
nbr.setColor('gray')
nbr.setDistance(currentVert.getDistance() + 1)
nbr.setPred(currentVert)
vertQueue.enqueue(nbr)
currentVert.setColor('black')
Теперь давайте посмотрим, как функция bfs конструирует дерево поиска в ширину относительно графа на рисунке 1. Начиная с “FOOL” мы берём все смежные с ним узлы и вставляем их в дерево. Такими узлами являются “POOL”, “FOIL”, “FOUL” и “COOL”. Так же каждый из них добавляется в очередь. Рисунок 3 показывает состояние дерева вместе с очередью после этого шага.
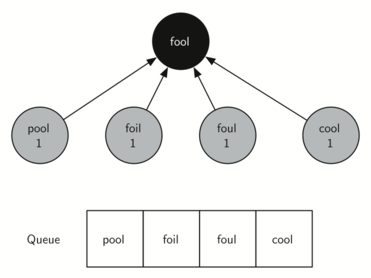
Рисунок 3: Первый шаг поиска в ширину.
На следующем шаге bfs из начала очереди удаляется очередной узел (“POOL”), и процесс повторяется для всех смежных с ним узлов. Однако, когда bfs проверяет узел “COOL”, она обнаруживает, что цвет этого узла уже был изменён на серый. Это говорит о том, что существует более короткий путь в “COOL” и что этот узел уже находится в очереди для дальнейшего рассмотрения. Единственным добавленным в очередь узлом при исследовании “COOL” стал “POLL”. Новое состояние очереди и дерева показано на рисунке 4.
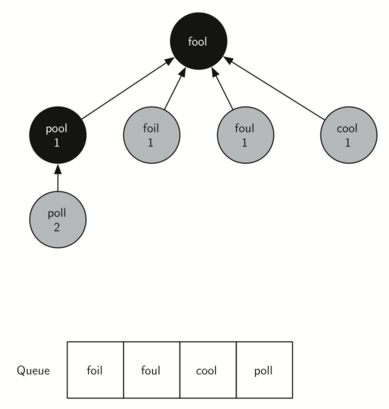
Рисунок 4: Второй шаг поиска в ширину.
Следующая вершина в очереди - “FOIL”. Единственным узлом, который она вставит в дерево, станет “FAIL”. После того, как bfs продолжит обрабатывать очередь, ни один из следующих двух узлов ничего нового не добавит. Рисунок 5 показывает очередь и дерево после исследования всех вершин второго уровня.
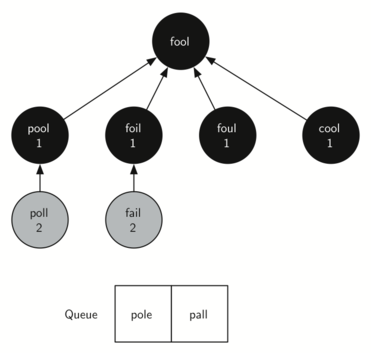
Рисунок 5: Поиск в ширину после заполнения первого уровня.
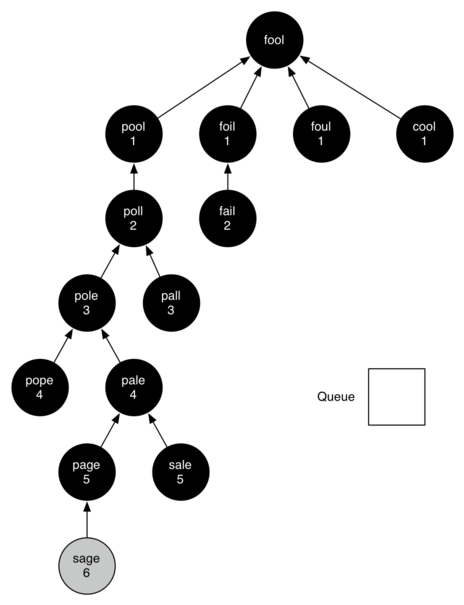
Рисунок 6: Итоговое дерево поиска в ширину
Вы можете продолжить работать по алгоритму самостоятельно, пока не почувствуете уверенное знание того, как он работает. Рисунок 6 показывает итоговое дерево поиска в ширину после того, как все вершины из рисунка 3 будут исследованы. Потрясающим моментом решения с помощью поиска в ширину является то, что мы решили не просто задачу “FOOL–SAGE”, с которой начинали, но и множество других. Мы можем начать с любой вершины дерева поиска в ширину и, пройдя по стрелкам предшественников в обратном направлении (к корню), найти кратчайшую словесную лестницу от любого слова до “FOOL”. Функция ниже (листинг 3) показывает, как пройти по ссылкам на предшественника, чтобы напечатать словесную лестницу.
Листинг 3
def traverse(y):
x = y
while (x.getPred()):
print(x.getId())
x = x.getPred()
print(x.getId())
traverse(g.getVertex('sage'))