Топологическая сортировка¶
В качестве демонстрации того, что учёные-информатики любую задачу могут свести к графу, давайте рассмотрим непростое задание напечь блинов. Рецепт очень прост: одно яйцо, одна чашка блинной смеси, одна столовая ложка растительного масла и \(3 \over 4\) чашки молока. Чтобы нажарить блинов, вам нужно разогреть сковородку, смешать вместе все ингредиенты и выливать смесь по ложке на горячую сковороду. Когда блин начинает пузыриться, переверните его и дождитесь, пока нижняя сторона не станет золотистой. Перед тем, как приступить к поеданию блинов, полейте их сиропом. Весь процесс показан в виде графа на рисунке 27.
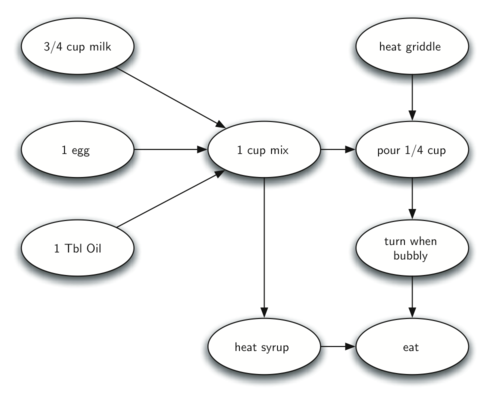
Рисунок 27: Этапы приготовления блинов
Трудность с приготовлением блинов состоит в необходимости определиться, что же делать первым. Как вы можете видеть на рисунке 27 , начинать можно с разогрева сковороды или добавления любого ингредиента в блинную смесь. Чтобы помочь нам определиться с порядком шагов для выпечки блинов, мы применим алгоритм на графах под названием топологическая сортировка.
Топологическая сортировка берёт направленный ацикличный граф и выдаёт такой линейный порядок всех его вершин, что если граф \(G\) содержит ребро \((v,w)\), то вершина \(v\) идёт перед вершиной \(w\). Направленный ацикличный граф используется во многих приложениях для указания приоритета событий. Приготовление блинов всего лишь один пример; к другим же можно отнести план проекта разработки программного обеспечения, приоритет графики для оптимизации запросов к базе данных и перемножение матриц.
Топологическя сортировка - простая, но полезная адаптация поиска в глубину. Её алгоритм следующий:
- Вызвать dfs(g) для некоего графа g. Основной причиной, по которой мы используем поиск в глубину, является необходимость подсчёта “времён” выхода для каждой из вершин.
- Сохранить вершины в списке в убывающем порядке их “времён” выхода.
- Вернуть упорядоченный список в качестве результата топологической сортировки.
На рисунке 28 показан лес поиска в глубину, сконструированный dfs по графу приготовления блинов из рисунка 26.
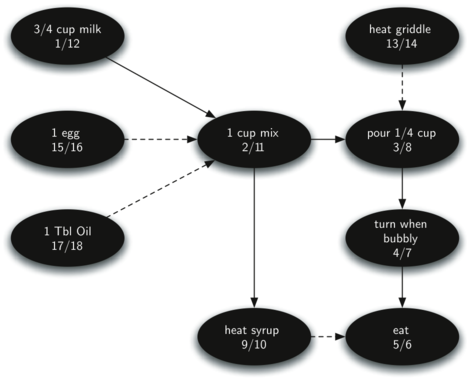
Рисунок 28: Результат поиска в глубину по блинному графу
Наконец, на рисунке 29 показаны результаты применения алгоритма топологической сортировки к нашему графу. Теперь все неоднозначности благополучно удалены, и мы знаем точный порядок этапов приготовления блинов.

Рисунок 29: Результат топологической сортировки направленного ацикличного графа