Вычисление суммы списка чисел¶

Начнём наше исследование с простой задачи, решение для которой вы уже знаете и без использования рекурсии. Предположим, вы хотите подсчитать сумму списка чисел \([1, 3, 5, 7, 9]\). Решение в виде итеративной функции показано в ActiveCode 1. Она использует переменную theSum в качестве аккумулятора, чьё начальное значение равно нулю и к которому прибавляются все числа из списка.

Представьте на минуту, что вы не можете использовать циклы while или for. Как бы вы подсчитали сумму чисел в списке? Если бы вы были математиками, то могли бы начать с того, что сложение - это функция, которая принимает два параметра (пару чисел). Чтобы переопределить задачу от сложения значений в списке к сложению пар чисел, мы перепишем список в виде выражения с полной расстановкой скобок. Выглядеть оно будет примерно так:

В прнципе, скобки можно расставить и в обратном порядке:

Обратите внимание, что самое внутренне выражение в скобках - \((7 + 9)\) - это задача, которую можно решить без использования циклов или каких-то специальных конструкций. Фактически, мы можем использовать следующую последовательность упрощений для вычисления итоговой суммы:

Осталось только переписать эту идею в виде программы на Python. Для начала, давайте заново сформулируем задачу сложения в терминах списков Python. Мы можем сказать, что что сумма списка numList - это сумма первого его элемента (numList[0]) и уже посчитанной суммы остатка списка (numList[1:]). В виде функции это выглядит так:

В этом выражении \(first(numList)\) возвращает первый элемент списка, а \(rest(numList)\) - список из оставшихся чисел. Это легко выражается в коде (см. ActiveCode 2):

Из этого листинга можно извлечь несколько ключевых моментов. Во-первых, в строке 2 мы проверяем, не является ли список единичным. Эта проверка имеет решающее значение и является “лазейкой” из функции. Нахождение суммы единичного списка - тривиальная задача. Ею будет значение единственного его элемента. Во-вторых, в строке 5 функция вызывает саму себя! Вот почему мы называем алгоритм listsum рекурсивным. Рекурсивная функция - это функция, вызывающая саму себя.

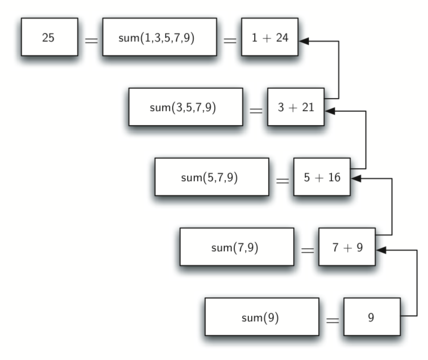
На рисунке 1 показана последовательность рекурсивных вызовов, которые требуются для подсчёта суммы списка \([1, 3, 5, 7, 9]\). Вы можете думать о ней, как о серии упрощений. Каждый раз, когда мы делаем рекурсивный вызов, мы решаем задачу меньшего размера до тех пор пока не достигнем точки, в которой её нельзя будет уменьшить.

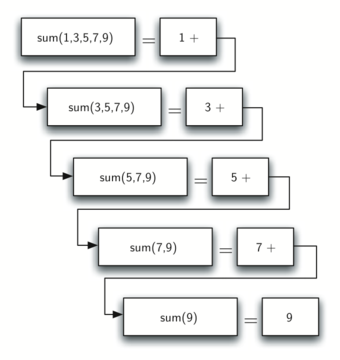
Когда мы достигаем точки максимального упрощения задачи, то начинаем собирать вместе кусочки решения каждой из маленьких подзадач до тех пор, пока они не сольются в решение первоначальной задачи. Рисунок 2 показывает операции сложения, которые выполняются во время работы listsum в обратном направлении по последовательности вызовов. Когда `listsum` вернёт ответ самой верхней задачи, мы будем иметь итоговое решение.