Exercises¶

Study the following source code:

def swap(x, y):      # incorrect version
     print("before swap statement: id(x):", id(x), "id(y):", id(y))
     x, y = y, x
     print "after swap statement: id(x):", id(x), "id(y):", id(y))

(a, b) = (0, 1)
print( "before swap function call: id(a):", id(a), "id(b):", id(b)
swap(a, b)
print("after swap function call: id(a):", id(a), "id(b):", id(b))

Run this program and describe the results. Use the results to explain why this version of swap does not work as intended. What will be the values of a and b after the call to swap?

Modify the Koch fractal program so that it draws a Koch snowflake, like this:
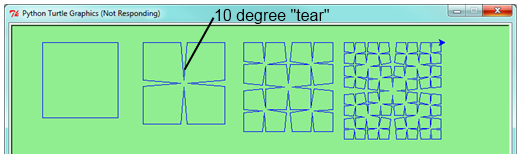
Draw a Cesaro torn square fractal, of the order given by the user. A torn square consists of four torn lines. We show four different squares of orders 0,1,2,3. In this example, the angle of the tear is 10 degrees. Varying the angle gives interesting effects — experiment a bit, or perhaps let the user input the angle of the tear.
A Sierpinski triangle of order 0 is an equilateral triangle. An order 1 triangle can be drawn by drawing 3 smaller triangles (shown slightly disconnected here, just to help our understanding). Higher order 2 and 3 triangles are also shown. Adapt the Koch snowflake program to draw Sierpinski triangles of any order input by the user.
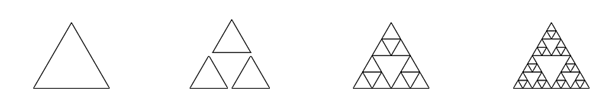
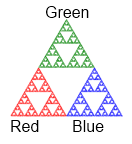
Adapt the above program to draw its three major sub-triangles in different colours, as shown here in this order 4 case:
Create a module named seqtools.py. Add the functions encapsulate and insert_in_middle from the chapter. Add tests which test that these two functions work as intended with all three sequence types.

Add each of the following functions to seqtools.py:

def make_empty(seq): pass
def insert_at_end(val, seq): pass
def insert_in_front(val, seq): pass
def index_of(val, seq, start=0): pass
def remove_at(index, seq): pass
def remove_val(val, seq): pass
def remove_all(val, seq): pass
def count(val, seq): pass
def reverse(seq): pass
def sort_sequence(seq): pass

def testsuite():
    test(make_empty([1, 2, 3, 4]), [])
    test(make_empty(('a', 'b', 'c')), ())
    test(make_empty("No, not me!"), '')

    test(insert_at_end(5, [1, 3, 4, 6]), [1, 3, 4, 6, 5])
    test(insert_at_end('x', 'abc'),  'abcx')
    test(insert_at_end(5, (1, 3, 4, 6)), (1, 3, 4, 6, 5))

    test(insert_in_front(5, [1, 3, 4, 6]),   [5, 1, 3, 4, 6])
    test(insert_in_front(5, (1, 3, 4, 6)),   (5, 1, 3, 4, 6))
    test(insert_in_front('x', 'abc'),        'xabc')

    test(index_of(9, [1, 7, 11, 9, 10]), 3)
    test(index_of(5, (1, 2, 4, 5, 6, 10, 5, 5)), 3)
    test(index_of(5, (1, 2, 4, 5, 6, 10, 5, 5), 4), 6)
    test(index_of('y', 'happy birthday'), 4)
    test(ndex_of('banana', ['apple', 'banana', 'cherry', 'date']), 1)
    test(index_of(5, [2, 3, 4]), -1)
    test(index_of('b', ['apple', 'banana', 'cherry', 'date']), -1)

    test(remove_at(3, [1, 7, 11, 9, 10]), [1, 7, 11, 10])
    test(remove_at(5, (1, 4, 6, 7, 0, 9, 3, 5)), (1, 4, 6, 7, 0, 3, 5))
    test(remove_at(2, "Yomrktown"), 'Yorktown')

    test(remove_val(11, [1, 7, 11, 9, 10]), [1, 7, 9, 10])
    test(remove_val(15, (1, 15, 11, 4, 9)), (1, 11, 4, 9))
    test(remove_val('what', ('who', 'what', 'when', 'where', 'why', 'how')),
          ('who', 'when', 'where', 'why', 'how'))

    test(remove_all(11, [1, 7, 11, 9, 11, 10, 2, 11]),  [1, 7, 9, 10, 2])
    test(remove_all('i', 'Mississippi'), 'Msssspp')

    test(count(5, (1, 5, 3, 7, 5, 8, 5)), 3)
    test(count('s', 'Mississippi'), 4)
    test(count((1, 2), [1, 5, (1, 2), 7, (1, 2), 8, 5]), 2)

    test(reverse([1, 2, 3, 4, 5]), [5, 4, 3, 2, 1])
    test(reverse(('shoe', 'my', 'buckle', 2, 1)), (1, 2, 'buckle', 'my', 'shoe'))
    test(reverse('Python'), 'nohtyP')

    test(sort_sequence([3, 4, 6, 7, 8, 2]),  [2, 3, 4, 6, 7, 8])
    test(sort_sequence((3, 4, 6, 7, 8, 2)),  (2, 3, 4, 6, 7, 8))
    test(sort_sequence("nothappy"), 'ahnoppty')

As usual, work on each of these one at a time until they pass all the tests.

But do you really want to do this?

Disclaimer. These exercises illustrate nicely that the sequence abstraction is general, (because slicing, indexing, and concatenation is so general), so it is possible to write general functions that work over all sequence types. Nice lesson about generalization!

Another view is that tuples are different from lists and strings precisely because you want to think about them very differently. It usually doesn’t make sense to sort the fields of the julia tuple we saw earlier, or to cut bits out or insert bits into the middle, even if Python lets you do so! Tuple fields get their meaning from their position in the tuple. Don’t mess with that.

Use lists for “many things of the same type”, like an enrollment of many students for a course.

Use tuples for “fields of different types that make up a compound record”.

Write a function, recursive_min, that returns the smallest value in a nested number list. Assume there are no empty lists or sublists:

test(recursive_min([2, 9, [1, 13], 8, 6]), 1)
test(recursive_min([2, [[100, 1], 90], [10, 13], 8, 6]), 1)
test(recursive_min([2, [[13, -7], 90], [1, 100], 8, 6]), -7)
test(recursive_min([[[-13, 7], 90], 2, [1, 100], 8, 6]), 13)

Write a function count that returns the number of occurences of target in a nested list:

test(count(2, []), 0)
test(count(2, [2, 9, [2, 1, 13, 2], 8, [2, 6]]), 4)
test(count(7, [[9, [7, 1, 13, 2], 8], [7, 6]]), 2)
test(count(15, [[9, [7, 1, 13, 2], 8], [2, 6]]), 0)
test(count(5, [[5, [5, [1, 5], 5], 5], [5, 6]]), 6)
test(count('a', [['this', ['a', ['thing', 'a'], 'a'], 'is'], ['a', 'easy']]), 5)

Write a function flatten that returns a simple list containing all the values in a nested list:

test(flatten([2, 9, [2, 1, 13, 2], 8, [2, 6]]), [2, 9, 2, 1, 13, 2, 8, 2, 6])
test(flatten([[9, [7, 1, 13, 2], 8], [7, 6]]), [9, 7, 1, 13, 2, 8, 7, 6])
test(flatten([[9, [7, 1, 13, 2], 8], [2, 6]]), [9, 7, 1, 13, 2, 8, 2, 6])
test(flatten([['this', ['a', ['thing'], 'a'], 'is'], ['a', 'easy']]),
              ['this', 'a', 'thing', 'a', 'is', 'a', 'easy'])
test(flatten([]), [])

Rewrite the fibonacci algorithm without using recursion. Can you find bigger terms of the sequence? Can you find fib(200)?
Write a function named readposint that uses the input dialog to prompt the user for a positive integer and then checks the input to confirm that it meets the requirements. It should be able to handle inputs that cannot be converted to int, as well as negative ints, and edge cases (e.g. when the user closes the dialog, or does not enter anything at all.)
Use help to find out what sys.getrecursionlimit() and sys.setrecursionlimit(n) do. Create several experiments similar to what was done in infinite_recursion.py to test your understanding of how these module functions work.
Write a program that walks a directory structure (as in the last section of this chapter), but instead of printing filenames, it returns a list of all the full paths of files in the directory or the subdirectories. (Don’t include directories in this list — just files.) For example, the output list might have elements like this:
```
['C:\Python31\Lib\site-packages\pygame\docs\ref\mask.html',
 'C:\Python31\Lib\site-packages\pygame\docs\ref\midi.html',
 ...
 'C:\Python31\Lib\site-packages\pygame\examples\aliens.py',
 ...
 'C:\Python31\Lib\site-packages\pygame\examples\data\boom.wav',
 ... ]
```
Write a program named litter.py that creates an empty file named trash.txt in each subdirectory of a directory tree given the root of the tree as an argument (or the current directory as a default). Now write a program named cleanup.py that removes all these files. Hint: Use the program from the example in the last section of this chapter as a basis for these two recursive programs. Because you’re going to destroy files on your disks, you better get this right, or you risk losing files you care about. So excellent advice is that initially you should fake the deletion of the files — just print the full path names of each file that you intent to delete. Once you’re happy that your logic is correct, and you can see that you’re not deleting the wrong