Быстрая сортировка¶

Быстрая сортировка использует технику “разделяй и властвуй”, чтобы получить те же преимущества, что и сортировка слиянием, но при этом не использовать дополнительное место. Однако, ценой за это станет то, что список может не поделиться пополам, приводя к уменьшению производительности.

Сначала быстрая сортировка выбирает значение, которое называется опорным элементом. Несмотря на то, что есть много способов выбрать его, мы будем просто использовать первое значение в списке. Роль опорного элемента заключается в помощи при разбиении списка. Позиция, на которой он окажется в итоговом сортированном списке, обычно называемая точкой разбиения, будет использоваться для разделения списка при последующих вызовах быстрой сортировки.

Рисунок 12 показывает, как 54 выступает в роли первого опорного значения. Поскольку мы уже рассматривали этот пример несколько раз, то знаем, что 54 в итоге окажется на позиции, занятой сейчас 31. Далее происходит процесс разделения. Он находит точку разделения и одновременно перемещает элементы по соответствующим сторонам списка, в зависимости от того, больше они или меньше опорной величины.

Разбиение начинается с определения двух маркеров положения - назовём их leftmark и rightmark - в начале и в конце оставшихся элементов списка (позиции 1 и 8 на рисунке 13). Целью процесса разбиения является перемещать элементы, лежащие по неправильным сторонам от опорного, пока они не сойдутся в точке разделения. Рисунок 13 показывает этот процесс, когда мы находимся на позиции 54-го элемента.

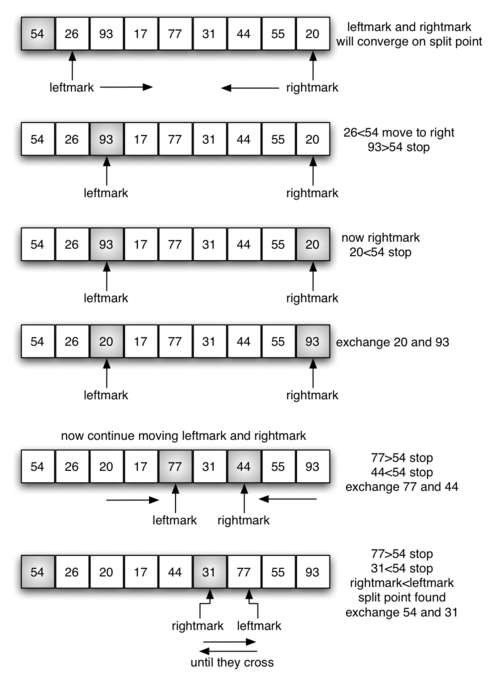
Мы начинаем с увеличения на единицу leftmark, пока не находим значение, большее опорного. Тогда мы уменьшаем на единицу rightmark, пока не находим значение, меньшее опорного. В этот момент мы имеем два элемента, находящихся на своих местах относительно итоговой точки разбиения. В нашем примере таковыми являются 93 и 20. Теперь можно поменять их местами и повторить процесс заново.

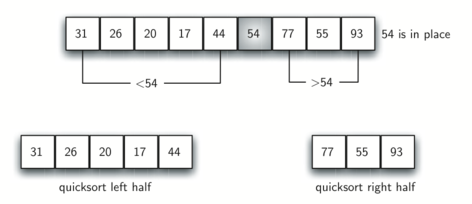
Когда rightmark становится меньше leftmark, мы останавливаемся. Позиция rightmark в данный момент - точка разбиения. Опорное значение следует поменять местами с её содержимым, и тогда оно будет стоять на своём месте (рисунок 14). В дополнение, все элементы слева от точки разбиения теперь меньше опорного значения, а справа - больше. Список поделен на две части, и быстрая сортировка может быть рекурсивно применена к каждой из них.

Функция quickSort, показанная в CodeLens 7, вызывает другую рекурсивную функцию - quickSortHelper. Она начинает рабоать с базового случая, аналогичного сортировке слиянием. Если длина списка меньше или равна единице, то он уже отсортирован. Если больше, то он может быть разделен и рекурсивно отсортирован. Функция partition воплощает описанный ранее процесс.

Для большей детализации, CodeLens 7 помогут вам пошагово пройти весь алгоритм.

Для анализа функции quickSort стоит отметить, что для списка длиной n, если деление приходится на его середину, мы вновь получим \(\log n\) разделений. С целью найти точку разбиения, каждый из n элементов нуждается в сравнении с опорным значением. Результатом станет \(n\log n\). При этом не требуется дополнительной памяти, как в сортировке слиянием.

К сожалению, в наихудшем случае точка разбиения может быть не по середине, а скакать слева направо, делая разделение очень неравномерным. В этом случае сортировка списка из n элементов разделится на сортировку списков размером 0 и \(n-1\) элементов. Далее сортировка списка длиной \(n-1\) опять даст подсписки из 0 и \(n-2\) элементов, и так далее. Результат: \(O(n^{2})\) со всеми накладными расходами, требуемыми для рекурсии.

Ранее мы упоминали, что есть несколько способов выбора опорного значения. В частности, мы можем попытаться сгладить потенциальный дисбаланс в разбиении с помощью метода, называемого медианой трёх. Чтобы выбрать опорное значение, мы рассматриваем первый, средний и последний элементы списка. В нашем примере это будут 54, 77 и 20. Теперь определим из них медиану - 54 в данном случае - и используем её в качестве опоры (естественно, это было опорное значение, которое мы использовали первоначально). Идея в том, что когда первый элемент списка не принадлежит его середине, медиана трёх станет лучшим “срединным” значением. Особенно это полезно, если первоначальный список уже подвергался частичной сортировке. Мы вам оставляем реализацию такого выбора опорного значения в качестве упражнения.