Сбалансированные деревья поиска¶

В предыдущем разделе мы рассмотрели построение двоичного дерева поиска. Как уже говорилось, при несбалансированности производительность его операций, подобных get и put, может деградировать до \(O(n)\). В этом разделе мы рассмотрим специальный вид двоичных деревьев, которые автоматически гарантируют неизменную сбалансированность. Их называют АВЛ-деревья (от имён изобретателей: Адельсон-Вельского Георгия Максимовича и Ландиса Евгения Михайловича).

АВЛ-дерево реализует АТД Map так же, как и обычное двоичное дерево поиска. Единственное отличие состоит в принципе работы дерева. Чтобы воплотить АВЛ-дерево, нам потребуется отслеживать фактор сбалансированности для каждого узла дерева. Мы будем делать это, следя за высотой левого и правого поддеревьев каждого из узлов. Более формально фактор сбалансированности для узла равен разнице между высотами его правого и левого поддеревьев.

Используя это определение, мы будем говрить, что дерево перевешивает влево, если фактор сбалансированности больше нуля, и вправо - если он меньше нуля. Если фактор равен нулю, то дерево сбалансировано идеально. При реализации АВЛ-дерева и использовании выгод от его сбалансированности, будем считать, что дерево сбалансировано, если фактор баланса равен -1, 0 или 1. Если же для какого-либо узла эта величина выходит за данный диапазон, то потребуется процедура возвращения дерева к сбалансированному состоянию. На рисунке 1 показан пример несбалансированного, перевешивающего вправо дерева и факторы сбалансированности для каждого из его узлов.

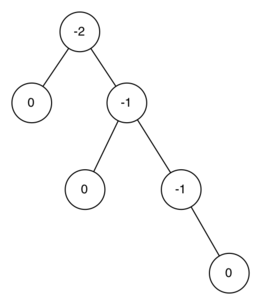
Рисунок 1: Несбалансированное, перевешивающее вправо дерево и факторы баланса для его узлов.