Реализация дерева поиска¶
Двоичные деревья поиска полагаются то, что ключи меньше родительского находятся в левом поддереве, а больше - в правом. Мы будем называть это bst-свойством (от англ. binary search tree - прим. переводчика). В процессе реализации описанного выше интерфейса Map оно станет нашим верным проводником. Рисунок 1 иллюстрирует это свойство двоичных деревьев поиска, показывая ключи без ассоциированных с ними значений. Обратите внимание, что таким свойством обладают и дети, и родители. Все ключи в левых поддеревьях меньше ключа корня, а в правых - больше, чем он.
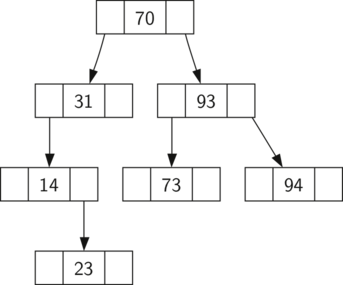
Рисунок 1: Простое двоичное дерево поиска
Теперь, когда вы знаете, что такое двоичное дерево поиска, можно рассмотреть процесс его создания. Дерево поиска на рисунке 1 содержит узлы, появившиеся после вставки следующих ключей в таком порядке: \(70,31,93,94,14,23,73\). Так как 70 - первый вставляемый в дерево ключ, то это корень. Число 31 меньше 70-и, поэтому оно уходит в левое поддерево. 93 наоборот больше - и вставляется в правое поддерево 70-и. Теперь у нас заполнены два уровня из трёх, так что следующий ключ должен стать правым или левым потомком 31 или 93. 94 больше, чем 70 и 93, поэтому мы делаем его правым потомком 93. Аналогично, 14 меньше и 70, и 31, следовательно, оно уходит в левое поддерево 31. 23 меньше, чем 31, так что оно тоже должно быть в левом поддереве 31. Однако, это число больше 14, следовательно, становится его правым потомком.
Для реализации двоичного дерева поиска мы используем узлы и ссылки (аналогично связанному списоку и дереву выражения). Однако, поскольку нам надо быть готовыми использовать двоичное дерево поиска и когда оно пусто, мы создадим два класса. Первый назовём BinarySearchTree, а второй - TreeNode. BinarySearchTree будет иметь ссылки на объект TreeNode, который является корнем дерева. В большинстве случаев внешние методы, определённые во внешнем классе, просто проверяют дерево на пустоту. Если у него есть узлы, то запрос просто передаётся в приватный метод, определённый в классе BinarySearchTree, который принимает корень в качестве параметра. В случае, когда дерево пусто или мы хотим удалить ключ из корня, необходимо предпринять специальные действия. Код для конструктора класса BinarySearchTree и нескольких других различных функций показан в листинге 1.
Листинг 1
class BinarySearchTree:
def __init__(self):
self.root = None
self.size = 0
def length(self):
return self.size
def __len__(self):
return self.size
def __iter__(self):
return self.root.__iter__()
Класс TreeNode предоставляет множество вспомогательных функций, которые значительно облегчают работу BinarySearchTree. Конструктор TreeNode вместе с этими функциями показан в листинге 2. Как вы можете из него видеть, большинство дополнительных функций помогают классифицировать узел в соответствии с его положением как потомка (левого или правого) и типом детей, которых он имеет.
Так же класс TreeNode явно отслеживает родителя, как атрибут каждого узла. Вы поймёте важность этого, когда мы будем обсуждать реализацию оператора del.
Другой любопытный аспект реализации TreeNode в листинге 2 заключается в использовании опциональных параметров Python. Они позволяют нам упростить создание TreeNode в соответствии с различными обстоятельствами. Иногда мы захотим сконструировать новый объект TreeNode, имеющий и parent, и child. С уже существующими потомком и предком мы можем просто передать их, как параметры. В следующий раз мы создадим TreeNode с парой ключ-значение, не передавая при этом ни parent, ни child. В этом случае для параметров будут использоваться значения по умолчанию.
Листинг 2
class TreeNode:
def __init__(self,key,val,left=None,right=None,
parent=None):
self.key = key
self.payload = val
self.leftChild = left
self.rightChild = right
self.parent = parent
def hasLeftChild(self):
return self.leftChild
def hasRightChild(self):
return self.rightChild
def isLeftChild(self):
return self.parent and self.parent.leftChild == self
def isRightChild(self):
return self.parent and self.parent.rightChild == self
def isRoot(self):
return not self.parent
def isLeaf(self):
return not (self.rightChild or self.leftChild)
def hasAnyChildren(self):
return self.rightChild or self.leftChild
def hasBothChildren(self):
return self.rightChild and self.leftChild
def replaceNodeData(self,key,value,lc,rc):
self.key = key
self.payload = value
self.leftChild = lc
self.rightChild = rc
if self.hasLeftChild():
self.leftChild.parent = self
if self.hasRightChild():
self.rightChild.parent = self
Теперь, когда у нас есть обёртка BinarySearchTree и класс TreeNode, пришло время написать метод put, который позволит строить двоичные деревья поиска. Он будет принадлежать классу BinarySearchTree. Метод будет выполнять проверку на наличие корня дерева, и если он отсутствует, то создавать объект TreeNode и устанавливать его, как корневой узел. В противном случае put вызовет приватную рекурсивную вспомогательную функцию _put для поиска места в дереве по следующему алгоритму:
- Начиная от корня, проходим по двоичному дереву, сравнивая новый ключ с ключом текущего узла. Если первый меньше второго, то идём в левое поддерево. Наоборот - в правое.
- Когда не осталось левых или правых потомков для поиска - мы нашли позицию для установки нового узла.
- Чтобы добавить узел в дерево, создаём новый объект TreeNode и помещаем его на найденное за предыдущие шаги место.
Листинг 3 показывает код Python для вставки нового узла в дерево. Функция _put написана рекурсивно и следует описанным выше пунктам. Отметьте, что когда в дерево вставляется новый потомок, currentNode передаётся как родитель нового дерева.
Одной из серьёзных проблем нашей реализации является то, что дубликаты ключей не обрабатываются правильным образом. В нашей реализации дубль создаст новый узел с точно таким же значением ключа и поместит его в правое поддерево узла с оригинальным ключом. В результате новый узел никогда не сможет быть обнаружен в процессе поиска. Лучший способ для управления вставкой дубликатов ключей: сделать так, чтобы значение, ассоциированное с новым ключом, заменяло старое. Мы оставляем вам исправление этого недочёта в качестве упражнения.
Листинг 3
def put(self,key,val):
if self.root:
self._put(key,val,self.root)
else:
self.root = TreeNode(key,val)
self.size = self.size + 1
def _put(self,key,val,currentNode):
if key < currentNode.key:
if currentNode.hasLeftChild():
self._put(key,val,currentNode.leftChild)
else:
currentNode.leftChild = TreeNode(key,val,parent=currentNode)
else:
if currentNode.hasRightChild():
self._put(key,val,currentNode.rightChild)
else:
currentNode.rightChild = TreeNode(key,val,parent=currentNode)
Определив метод put, можно легко перегрузить оператор [] для присвоения с помощью вызова метода __setitem__ (см. листинг 4). Это позволит нам писать выражения вида myZipTree['Plymouth'] = 55446, как для словарей Python.
Листинг 4
def __setitem__(self,k,v):
self.put(k,v)
Рисунок 2 иллюстрирует процесс вставки нового узла в двоичное дерево поиска. Слегка затенённые узлы показывают узлы, посещённые во время процесса вставки.
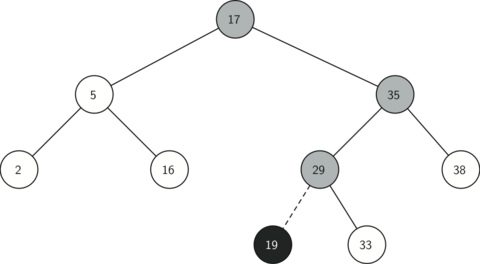
Рисунок 2: Вставка узла с ключом, равным 19.
Самопроверка
Поскольку дерево уже сконструировано, то следующее задание - реализовать поиск значения по заданному ключу. Метод get проще put, потому что просто делает рекурсивный поиск, пока не дойдёт до листового узла или не найдёт искомое. Когда ключ найдётся, хранимое в полезной нагрузке значение будет возвращено.
Листинг 5 демонстрирует код для get, _get и __getitem__. Код поиска в методе _get``использует ту же логику для выбора правого или левого потомка, что и ``_put. Обратите внимание, _get возвращает в get объект TreeNode. Это позволяет использовать _get в качестве гибкого вспомогательного метода для других методов BinarySearchTree, которым могут потребоваться другие данные из TreeNode, кроме полезной нагрузки.
Реализовав метод __getitem__, мы можем писать операторы Python, выглядящие так, будто мы имеем доступ к словарю, когда по факту используется двоичное дерево поиска. Например, z = myZipTree['Fargo']. Как вы можете видеть, всё, что делает __getitem__, - это вызывает get.
Листинг 5
def get(self,key):
if self.root:
res = self._get(key,self.root)
if res:
return res.payload
else:
return None
else:
return None
def _get(self,key,currentNode):
if not currentNode:
return None
elif currentNode.key == key:
return currentNode
elif key < currentNode.key:
return self._get(key,currentNode.leftChild)
else:
return self._get(key,currentNode.rightChild)
def __getitem__(self,key):
return self.get(key)
С использованием get можно реализовать операцию in, написав метод __contains__ для BinarySearchTree. Он будет просто вызывать get и выдавать True, если get возвращает значение, или False в противном случае. Код для __contains__ показан в листинге 6.
Листинг 6
def __contains__(self,key):
if self._get(key,self.root):
return True
else:
return False
Напомним, что __contains__ перегружает оператор in и позволяет писать код наподобие
if 'Northfield' in myZipTree:
print("oom ya ya")
В завершение обратим наше внимание на наиболее сложный метод для двоичного дерева поиска - удаление ключа (см. листинг 7). Первым заданием будет поиск в дереве удаляемого узла. Если дерево имеет больше одного узла, то для этого используется метод _get. Если же оно состоит из единственного узла, то это подразумевает удаление корня. Однако, проверить корневой ключ на соответствие удаляемому всё же будет необходимо. В обоих случаях, если ключ не найден, то оператор del выдаёт ошибку.
Листинг 7
def delete(self,key):
if self.size > 1:
nodeToRemove = self._get(key,self.root)
if nodeToRemove:
self.remove(nodeToRemove)
self.size = self.size-1
else:
raise KeyError('Error, key not in tree')
elif self.size == 1 and self.root.key == key:
self.root = None
self.size = self.size - 1
else:
raise KeyError('Error, key not in tree')
def __delitem__(self,key):
self.delete(key)
После того, как мы нашли ключ, содержащий значение, которое хотим удалить, существует три варианта, которые следует рассмотретьпо отдельности:
- Удаляемый узел не имеет потомков (см. рисунок 3).
- У удаляемого узла есть только один потомок (см. рисунок 4).
- У удаляемого узла есть два потомка (см. рисунок 5).
В первом случае всё очевидно (см. листинг 8). Если текущий узел не имеет потомков, то всё, что от нас требуется, - это удалить его и ссылку на него у его родителя. Вот код для этого:
Листинг 8
if currentNode.isLeaf():
if currentNode == currentNode.parent.leftChild:
currentNode.parent.leftChild = None
else:
currentNode.parent.rightChild = None
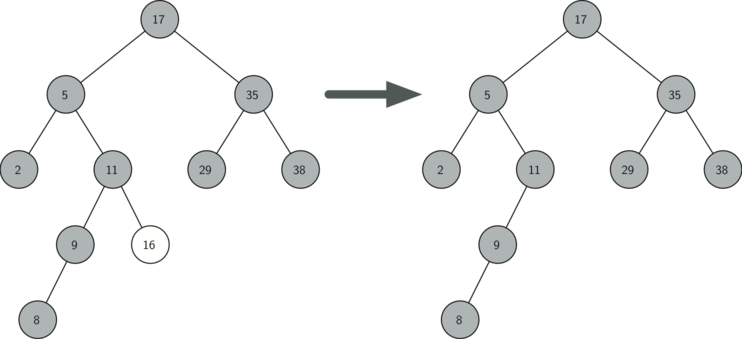
Рисунок 3: Удаление узла 16, не имеющего потомков
Второй случай ненамного сложнее (см. листинг 9). Если у узла всего один потомок, то мы просто поможем ему занять место родителя. Код для этого показан в следующем листинге. В нём вы можете видеть, что есть шесть случаев для рассмотрения. Поскольку они симметричны для левого и правого потомков, мы обсудим только вариант, когда узел имеет левого потомка. Процесс поиска решения следующий:
- Если текущий узел - левый потомок, то нужно всего лишь обновить родительскую ссылку на левого потомка у родителя текущего узла, а затем обновить ссылку потомка, чтобы она указывала на нового родителя.
- Если текущий узел - правый потомок, то мы обновляем его родительскую ссылку, чтобы она указывала на родителя текущего узла, а затем - ссылку на правого потомка у родителя текущего узла.
- Если текущий узел родителя не имеет, то он должен быть корнем. В этом случае мы просто заменяем данные key, payload, leftChild и rightChild, вызвав для корня метод replaceNodeData.
Листинг 9
else: # this node has one child
if currentNode.hasLeftChild():
if currentNode.isLeftChild():
currentNode.leftChild.parent = currentNode.parent
currentNode.parent.leftChild = currentNode.leftChild
elif currentNode.isRightChild():
currentNode.leftChild.parent = currentNode.parent
currentNode.parent.rightChild = currentNode.leftChild
else:
currentNode.replaceNodeData(currentNode.leftChild.key,
currentNode.leftChild.payload,
currentNode.leftChild.leftChild,
currentNode.leftChild.rightChild)
else:
if currentNode.isLeftChild():
currentNode.rightChild.parent = currentNode.parent
currentNode.parent.leftChild = currentNode.rightChild
elif currentNode.isRightChild():
currentNode.rightChild.parent = currentNode.parent
currentNode.parent.rightChild = currentNode.rightChild
else:
currentNode.replaceNodeData(currentNode.rightChild.key,
currentNode.rightChild.payload,
currentNode.rightChild.leftChild,
currentNode.rightChild.rightChild)
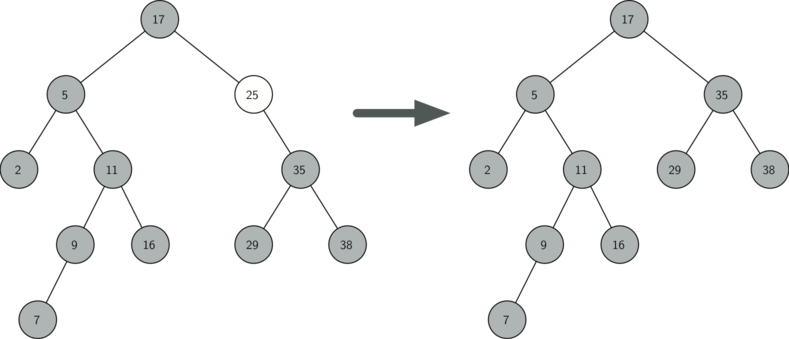
Рисунок 4: Удаление узла 25, имеющего единственного потомка.
Третий случай наиболее сложный для обработки (см. листинг 10). Если у узла есть оба потомка, то маловероятно, что можно просто поставить их на место родителя. Однако, мы можем пройти поиском по дереву и найти узел, способный заменить тот, который стоит в списке на выбывание. Нам нужно, чтобы этот узел сохранял принятые в двоичном дереве поиска отношения между существующими правым и левым поддеревьями. Способный на это узел будет иметь следующий по величине ключ. Мы назовём его преемником и рассмотрим способ найти как можно быстрее. Преемник гарантированно имеет не более, чем одного потомка, так что мы знаем, как можно его удалить с использованием двух уже рассмотренных и написанных случаев. Как только преемник будет удалён, мы просто вставим его в дерево на место удаляемого узла.
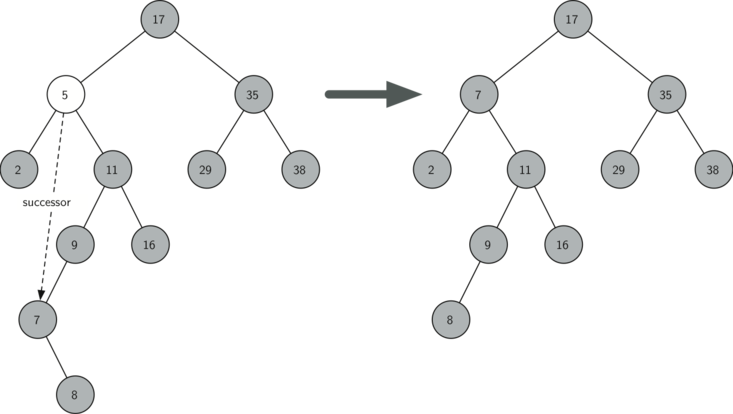
Рисунок 5: Удаление узла 5, имеющего двух потомков.
Код, обрабатывающий третий случай, показан в следующем листинге. Обратите внимание на использование вспомогательных методов findSuccessor и findMin для поиска преемника. Чтобы его удалить, мы применяем метод spliceOut. Причина, по которой это делается, состоит в том, что он идёт точно в тот узел, который мы хотим соединить, и осуществляет правильную замену. Можно было бы рекурсивно вызвать delete, но это означает пустую трату времени на повторный поиск ключевого узла.
Листинг 10
elif currentNode.hasBothChildren(): #interior
succ = currentNode.findSuccessor()
succ.spliceOut()
currentNode.key = succ.key
currentNode.payload = succ.payload
Код для поиска преемника показан ниже (см. листинг 11) и, как вы можете видеть, это метод класса``TreeNode``. Этот код использует те же свойства двоичных деревьев поиска, что и при распечатке узлов от меньшего к большему при симметричном обходе. Вот три случая, которые следует рассмотреть при поиске преемника:
- Если у узла есть правый потомок, то преемник - наименьший ключ в правом поддереве.
- Если у узла нет правого потомка и он левый потомок родителя, то преемником будет родитель.
- Если узел - правый потомок своего родителя и сам правого потомка не имеет, то его преемником будет преемник родителя (исключая сам этот узел).
Первое условие - единственное имеющее для нас значение при удалении узла из двоичного дерева поиска. Однако, метод findSuccessor имеет ещё одно применение, которое будет исследовано в упражнениях в конце этой главы.
Метод findMin вызывается для поиска минимального ключа в дереве. Вам следует самостоятельно убедиться, что минимальный ключ в любом двоичном дереве поиска - самый левый из потомков. Поэтому метод findMin всего лишь следует по ссылкам ``leftChild` до тех пор, пока не достигнет узла, не имеющего левых потомков.
Листинг 11
def findSuccessor(self):
succ = None
if self.hasRightChild():
succ = self.rightChild.findMin()
else:
if self.parent:
if self.isLeftChild():
succ = self.parent
else:
self.parent.rightChild = None
succ = self.parent.findSuccessor()
self.parent.rightChild = self
return succ
def findMin(self):
current = self
while current.hasLeftChild():
current = current.leftChild
return current
def spliceOut(self):
if self.isLeaf():
if self.isLeftChild():
self.parent.leftChild = None
else:
self.parent.rightChild = None
elif self.hasAnyChildren():
if self.hasLeftChild():
if self.isLeftChild():
self.parent.leftChild = self.leftChild
else:
self.parent.rightChild = self.leftChild
self.leftChild.parent = self.parent
else:
if self.isLeftChild():
self.parent.leftChild = self.rightChild
else:
self.parent.rightChild = self.rightChild
self.rightChild.parent = self.parent
Нам осталось рассмотреть последний метод интерфейса для двоичного дерева поиска. Предположим, вы просто хотите перебрать все ключи в дереве по порядку. Это определённо то, что мы делаем со словарями, так почему бы не сделать это и с деревом? Вы уже знаете, как обходить двоичное дерево по порядку с использованием алгоритма обхода inorder. Однако, написание итератора поребует немного больше работы, поскольку он должен возвращать только один узел за каждый свой вызов.
Для создания итератора Python предоставляет очень мощную функцию под названием yield. Она аналогична return, возвращающему значение вызывающему коду. Однако, yield так же делает дополнительный шаг, замораживая состояние функции, чтобы когда она будет вызвана в следующий раз, вычисления продолжились с оставленного места. Функция, создающая объект, который может быть итерирован, называется генератором функций.
Код для итератора inorder двоичного дерева показан в следующем листинге. Посмотрите на него внимательнее: на первый взгляд может показаться, будто он не рекурсивный. Однако, вспомните, что __iter__ перегружает опреацию for x in для итерирования. Так что на самом деле рекурсия здесь есть. Поскольку код рекурсивен для объектов TreeNode, метод __iter__ определён в классе TreeNode.
def __iter__(self):
if self:
if self.hasLeftChild():
for elem in self.leftChiLd:
yield elem
yield self.key
if self.hasRightChild():
for elem in self.rightChild:
yield elem
Сейчас вы можете захотеть целиком загрузить файл, содержащий полную версию классов BinarySearchTree и TreeNode.
(completebstcode)