Обход дерева¶

После того, как мы испытали функционал нашего дерева, пришло время расмотреть некоторые дополнительные модели использования этой структуры. Их можно разделить по трём способам доступа к узлам дерева. Разница между этими моделями - в порядке посещения каждого узла. Мы будем называть посещение узлов словом “обход”. Три способа обхода, которые мы рассмотрим, называются обход в прямом порядке, симметричный обход и обход в обратном порядке. Начнём с того, что дадим им более тщательные определения, а затем рассмотрим несколько примеров, где эти модели будут полезны.

Обход в прямом порядке

В этом случае мы сначала посещаем корневой узел, затем рекурсивно обходим в прямом порядке левое поддерево, после чего таким же образом обходим правое.

Симметричный обход

Сначала мы симметрично обходим левое поддерево, затем посещаем корневой узел, затем - правое поддерево.

Обход в обратном порядке

Сначала делается рекурсивный обратный обход левого и правого поддеревьев, после чего посещается корневой узел.

Рассмотрим несколько примеров, иллюстрирующих каждый из этих типов обхода. Первым будет обход в прямом порядке. В качестве примера дерева возьмём эту книгу. Сама по себе она является корнем, чьи потомки - главы. Каждый раздел главы будет уже её потомком, каждый подраздел - потомком раздела и так далее. Рисунок 5 показывает урезанную версию книги (всего две главы). Обратите внимание, что алгоритм обхода будет работать с любым числом потомков, но мы пока сосредоточимся на двоичном дереве.

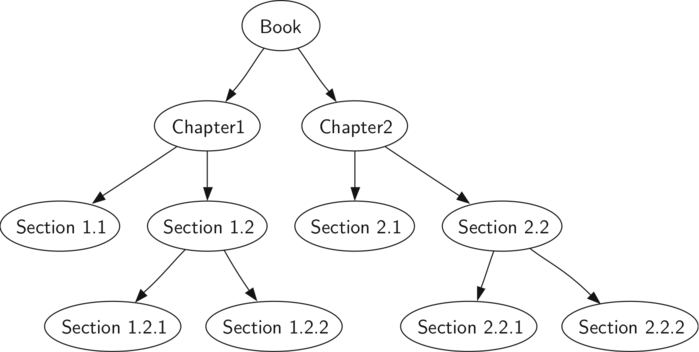
Рисунок 5: Представление книги в виде дерева

Предположим, вы хотите прочитать эту книгу от начала до конца. Обход в прямом порядке даст вам в точности такую последовательность. Начиная с корня дерева (узел Book), последуем инструкциям прямого обхода. Мы рекурсивно вызовем preorder к левому потомку (Chapter1), а потом к его левому потомку (Section 1.1). Section 1.1 является листом, так что больше рекурсивные вызовы не нужны. Закончив с ней, мы поднимемся по дереву вверх до Chapter 1. Нам по-прежнему надо посетить правое поддрево - Section 1.2. Как и раньше, сначала мы пойдём по его левому потомку (1.2.1), а затем посетим узел Section 1.2.2. Закончив с Section 1.2, мы вернёмся к Chapter 1, потом к Book и проделаем аналогичную процедуру для Chapter 2.

Код для описанного обхода дерева на удивление элегантный - в основном благодаря рекурсии. Листинг 2 демонстрирует код прямого обхода двоичного дерева.

Может возникнуть вопрос: в каком виде лучше написать алгоритм вроде обхода в прямом порядке? Должна ли это быть функция, просто использующая дерево как структуру данных, или это будет метод внутри класса “дерево”? В листинге 2 показан вариант с внешней функцией, принимающей двоичное дерево в качестве параметра. В частности, элегантность такой функции заключается в базовом случае - проверке существования дерева. Если её параметр равен None, то она возвращается без выполнения каких-либо действий.

Листинг 2

def preorder(tree):
    if tree:
        print(tree.getRootVal())
        preorder(tree.getLeftChild())
        preorder(tree.getRightChild())

preorder также можно реализовать, как метод класса BinaryTree. Код preorder в качестве внутреннего метода показан в листинге 3. Обратите внимание, что происходит, когда мы перемещаем код “снаружи” “внутрь”. В общем, мы просто меняем tree на self. Однако, так же требуется изменить и базовый случай. Внутренний метод проверяет наличие левого и правого потомков до того, как делает рекурсивный вызов preorder.

Листинг 3

def preorder(self):
    print(self.key)
    if self.leftChild:
        self.left.preorder()
    if self.rightChild:
        self.right.preorder()

Какой из двух способов реализации preorder лучше? Ответ: для данного случая preorder, как внешняя функция, будет лучшим решением. Причина в том, что вы очень редко хотите просто обойти дерево. В большинстве случаев вам нужно сделать что-то ещё во время использования одной из моделей обхода. Фактически, уже в следующем примере мы увидим, что модель обхода postorder очень близка к коду, который мы писали ранее для вычисления дерева синтаксического разбора. Исходя из изложенного, для оставшихся моделей мы будем писать внешние функции.

Алгоритм обхода postorder показан в листинге 4. Он очень близок к preorder, за исключением того, что мы перемещаем вызов печати в конец функции.

Листинг 4

def postorder(tree):
    if tree != None:
        postorder(tree.getLeftChild())
        postorder(tree.getRightChild())
        print(tree.getRootVal())

Мы уже видели распространённое использование обхода в обратном порядке - вычисление дерева синтаксического разбора. Взгляните на листинг 1 ещё раз. Что мы делаем, так это вычисляем левое поддерево, потом правое и собираем их в корне через вызов функции оператора. Предположим, наше двоичное дерево будет хранить только данные для математического выражения. Давайте перепишем функцию вычисления более приближённо к коду postorder из листинга 4 (см. листинг 5).

Листинг 5

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

def postordereval(tree):
    opers = {'+':operator.add, '-':operator.sub, '*':operator.mul, '/':operator.truediv}
    res1 = None
    res2 = None
    if tree:
        res1 = postordereval(tree.getLeftChild())
        res2 = postordereval(tree.getRightChild())
        if res1 and res2:
            return opers[tree.getRootVal()](res1,res2)
        else:
            return tree.getRootVal()

Обратите внимание, что форма в листинге 4 аналогична форме в листинге 5, за исключением того, что вместо печати ключей в конце функции, мы их возвращаем. Это позволяет сохранить значения, возвращаемые рекурсивными вызовами в строках 6 и 7. Затем они используются вместе с оператором в строке 9.

Последним рассмотренным в этом разделе обходом будет симметричный обход. В его ходе мы сначала посещаем левое поддерево, затем корень и потом уже правое поддерево. Листинг 6 показывает этот алгоритм в коде. Заметьте, что во всех трёх моделях обхода мы просто меняем расположение оператора print по отношению к двум рекурсивным вызовам.

Листинг 6

def inorder(tree):
  if tree != None:
      inorder(tree.getLeftChild())
      print(tree.getRootVal())
      inorder(tree.getRightChild())

Если мы применим простой симметричный обход к дереву синтаксического разбора, то получим оригинальное выражение, правда без скобок. Давайте модифицируем базовый алгоритм симметричного обхода, чтобы он позволял восстановить версию выражения с полной расстановкой скобок. Единственное изменение, которое надо внести в базовый шаблон, - это печатать левую скобку до рекурсивного вызова с левым поддеревом и правую скобку после рекурсивного вызова с правым поддеревом. Модифицированный код показан в листинге 7.

Листинг 7

def printexp(tree):
  sVal = ""
  if tree:
      sVal = '(' + printexp(tree.getLeftChild())
      sVal = sVal + str(tree.getRootVal())
      sVal = sVal + printexp(tree.getRightChild())+')'
  return sVal

Обратите внимание, что функция printexp после реализации помещает скобки вокруг каждого числа. Не то, чтобы это было неправильно, но они здесь просто не нужны. В упражнении в конце этой главы вас попросят изменить printexp, чтобы исправить это.