Реализация АВЛ-дерева¶

Теперь, когда мы показали, что поддержка баланса АВЛ-дерева даёт огромное улучшение производительности, давайте посмотрим, как можно расширить процедуру вставки в дерево нового ключа. Поскольку все ключи вставляются, как листья, и известно, что фактор сбалансированности нового листа равен нулю, то к свежевставленному узлу никаких дополнительных требваний не предъявляется. Однако, если добавлен новый лист, то надо обновить фактор сбалансированности его родителя. То, как вставленный узел на него повлияет, зависит от того, является он левым или правым потомком. Если лист - правый потомок, то фактор баланса уменьшится на единицу, если левый - то увеличится на один. Это отношение может быть рекурсивно применено к деду нового узла и, вполне возможно, к каждому из его предков вплоть до корня дерева. Поскольку это рекурсивная процедура, то давайте рассмотрим два базовых случая для обновления фактора сбалансированности:

Рекурсивный вызов достиг корня дерева.
Фактор баланса родителя скорректировался до нуля. Докажите самостоятельно, что если поддерево имеет фактор сбалансированности, равный нулю, то баланс его узла-предка не изменяется.

Мы будем воплощать АВЛ-дерево как подкласс BinarySearchTree. Для начала перегрузим метод _put и напишем новую вспомогательную функцию updateBalance. Код показан в листинге 1. Из него видно, что определение _put осталось в точности таким, как и для простого двоичного дерева, за исключением дополнительных вызовов updateBalance в строках 7 и 13.

Листинг 1

def _put(self,key,val,currentNode):
  if key < currentNode.key:
      if currentNode.hasLeftChild():
        self._put(key,val,currentNode.leftChild)
      else:
        currentNode.leftChild = TreeNode(key,val,parent=currentNode)
        self.updateBalance(currentNode.leftChild)
  else:
      if currentNode.hasRightChild():
        self._put(key,val,currentNode.rightChild)
      else:
        currentNode.rightChild = TreeNode(key,val,parent=currentNode)
        self.updateBalance(currentNode.rightChild)

def updateBalance(self,node):
  if node.balanceFactor > 1 or node.balanceFactor < -1:
      self.rebalance(node)
      return
  if node.parent != None:
      if node.isLeftChild():
        node.parent.balanceFactor += 1
      elif node.isRightChild():
        node.parent.balanceFactor -= 1

      if node.parent.balanceFactor != 0:
        self.updateBalance(node.parent)

Большая часть работы совершается в новом методе updateBalance. Здесь реализована рекурсивная процедура, описанная выше. Сначала метод проверяет, потерял ли узел баланс настолько, что требуется новая балансировка. Если без этого можно обойтись, то фактор баланса родителя просто корректируется. В случае, когда его значение отлично от нуля, алгоритм продолжает работу вверх по дереву, рекурсивно вызывая updateBalance для предка текущего узла.

Но как мы будем делать балансировку, если она нужна? Эффективное восстановление баланса - ключ, позволяющий АВЛ-дереву хорошо работать без ущерба для производительности. Чтобы вернуть дерево в состояние баланса, мы сделаем одно или несколько его вращений.

Чтобы разобраться в этом, рассмотрим очень простой пример. Посмотрите на левую половину дерева на рисунке 3. Она разбалансирована (фактор баланса -2), и для исправления мы повернём влево поддерево с корнем в узле А.

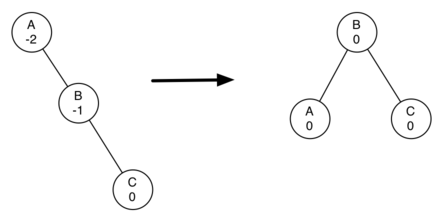
Рисунок 3: Трансформация разбалансированного дерева с помощью левого поворота.

По существу, для выполнения левого вращения надо сделать следующее:

Продвинуть правого потомка (В), чтобы он стал корнем поддерева.
Переместить старый корень (А) на место левого потомка нового корня поддерева.
Если новый корень (В) уже имеет левого потомка, то сделать последнего правым потомком узла А. Отметьте: поскольку новый корень (В) был правым сыном А, то это место теперь гарантированно пусто, что позволяет добавлять вправо новый узел без дальнейших рассуждений.

Хотя концепция процедуры достаточно проста, отдельные части кода будут несколько каверзными, поскольку нам придётся перемещать узлы в правильном порядке, сохранив все свойства двоичного дерева поиска. Более того, мы должны убедиться, что правильно обновили все родительские указатели.

Рассмотрим чуть более сложное дерево, иллюстрируюшее правое вращение. Левая часть рисунка 4 показывает дерево, перевешивающее влево, с фактором сбалансированности корня равным 2. Чтобы выполнить правое вращение, надо сделать следующее:

Продвинуть левого потомка (С), чтобы он стал корнем поддерева.
Передвинуть старый корень (Е) на место правого потомка нового корня.
Если новый корень (С) уже имеет правого потомка (D), то сделать последнего левым потомком Е. Замечание: поскольку новый корень (С) был левым потомком Е, то это место гарантированно остаётся пустым, что позволяет нам без рассуждений добавлять новому узлу левого потомка.

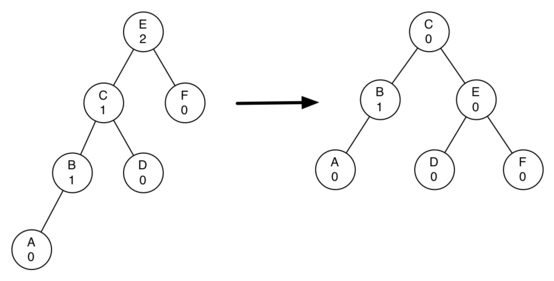
Рисунок 4: Преобразование разбалансированного дерева с помощью поворота вправо

После того, как вы познакомились с идеей вращения и принципами его работы, давайте посмотрим на код. Листинг 2 содержит код для левого вращения. В строке 2 мы создаём временную переменную, которая будет отслеживать новый корень поддерева. Как мы уже говорили, им становится правый потомок предыдущего корня. Теперь, когда ссылка сохранена во временной переменной, мы можем заменить правого потомка старого корня левым потомком нового.

Следующим шагом станет корректировка родительских указателей двух узлов. Если у newRoot есть левый потомок, то его новым предком станет старый корень. Родителем нового корня устанавливается предок старого. Если старый корень был корнем всего дерева, то необходимо переустановить главный указатель на новый корень. В противном случае (старый корень - левый потомок) мы меняем указатель родителя левого потомка таким образом, чтобы он указывал на новый корень. Если старый корень - правый потомок, то на новый корень должен ссылаться указатель правого потомка (строки 10-13).

Наконец, мы устанавливаем родителем старого корня новый корень. Это не самая лёгкая бухгалтерия, так что мы рекомендуем вам пошагово пройти эту функцию с помощью рисунка 3. Метод rotateRight симметричен rotateLeft, так что его мы оставляем на самостоятельное изучение.

Листинг 2

def rotateLeft(self,rotRoot):
  newRoot = rotRoot.rightChild
  rotRoot.rightChild = newRoot.leftChild
  if newRoot.leftChild != None:
      newRoot.leftChild.parent = rotRoot
  newRoot.parent = rotRoot.parent
  if rotRoot.isRoot():
      self.root = newRoot
  else:
      if rotRoot.isLeftChild():
        rotRoot.parent.leftChild = newRoot
      else:
        rotRoot.parent.rightChild = newRoot
  newRoot.leftChild = rotRoot
  rotRoot.parent = newRoot
  rotRoot.balanceFactor = rotRoot.balanceFactor + 1 - min(newRoot.balanceFactor, 0)
  newRoot.balanceFactor = newRoot.balanceFactor + 1 + max(rotRoot.balanceFactor, 0)

Строки 16-17 требуют некоторых пояснений. В них мы обновляем факторы сбалансированности старого и нового корней. Поскольку все прочие перемещения затрагивают поддеревья целиком, то на факторы баланса остальных узлов поворот влияния не оказывает. Но как можно обновить факторы сбалансированности без полного пересчёта высот новых поддеревьев? Следующее доказательство убедит вас в корректности нашего кода.

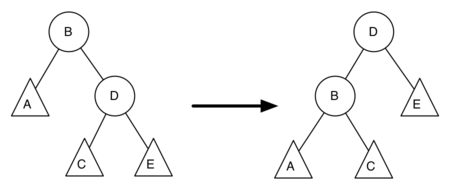
Рисунок 5: Поворот влево

Рисунок 5 показывает левое вращение. В и D - опорные узлы, A, C и E - их поддеревья. Пусть \(h_x\) обозначает высоту конкретного дерева с корнем в узле \(x\). По определению мы знаем:

\[\begin{split}newBal(B) = h_A - h_C \\ oldBal(B) = h_A - h_D\end{split}\]

Но мы также знаем, что старая высота D тоже может быть задана \(1 + max(h_C,h_E)\). Следовательно, высота D не превышает максимальной из высот его потомков. Вспомните: \(h_c\) и \(h_E\) не меняются. Таким образом, их можно заменить во втором уравнении, что даст нам

\(oldBal(B) = h_A - (1 + max(h_C,h_E))\) ,

а затем вычесть одно уравнение из другого. На следующих этапах производится вычитание и используется немного простой алгебры, чтобы упростить выражение для \(newBal(B)\).

\[\begin{split}newBal(B) - oldBal(B) = h_A - h_C - (h_A - (1 + max(h_C,h_E))) \\ newBal(B) - oldBal(B) = h_A - h_C - h_A + (1 + max(h_C,h_E)) \\ newBal(B) - oldBal(B) = h_A - h_A + 1 + max(h_C,h_E) - h_C \\ newBal(B) - oldBal(B) = 1 + max(h_C,h_E) - h_C\end{split}\]

Далее мы перенесём \(oldBal(B)\) в правую часть уравнения и воспользуемся тем, что \(max(a,b)-c = max(a-c, b-c)\).

\[\begin{split}newBal(B) = oldBal(B) + 1 + max(h_C - h_C ,h_E - h_C) \\\end{split}\]

Но \(h_E - h_C\) - это то же самое, что \(-oldBal(D)\). Поэтому мы можем использовать другую замену, говорящую \(max(-a,-b) = -min(a,b)\). Таким образом, наше доказательство для \(newBal(B)\) заканчивается следующими шагами:

\[\begin{split}newBal(B) = oldBal(B) + 1 + max(0 , -oldBal(D)) \\ newBal(B) = oldBal(B) + 1 - min(0 , oldBal(D)) \\\end{split}\]

Теперь у нас есть все части в известных терминах. Если вы помните, В - это rotRoot, а D - newRoot. Так что эти соотношения в точности повторяет присваивание в строке 16:

rotRoot.balanceFactor = rotRoot.balanceFactor + 1 - min(0,newRoot.balanceFactor)

Аналогичное доказательство даст нам выражение для обновления узла D и факторов сбалансированности после правого поворота. Мы оставляем его вам в качестве упражнения.

Теперь вы могли бы подумать, что дело сделано. Мы знаем, как и когда применять правое и левое вращения, но взгляните на рисунок 6. Поскольку узел А имеет фактор сбалансированности равный -2, нам следует выполнить поворот влево. Но что произойдёт, когда мы сделаем левое вращение вокруг А?

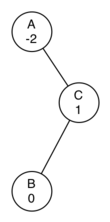
Рисунок 6: Разбалансированное дерево, которое сложнее отбалансировать

Рисунок 7 показывает, что после левого вращения дисбаланс сохраняется, хоть и по-другому. Если мы сделаем поворот вправо для коррекции ситуации, то вернёмся к тому, откуда начали.

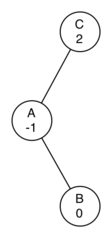
Рисунок 7: После левого поворота дерево осталось несбалансированным, но в другом направлении

Для корректировки этой проблемы нам нужно использовать следующий набор правил:

Если поддерево для восстановления баланса требует поворота влево, прежде следует проверить фактор сбалансированности его правого потомка. Если он перевешивает влево - повернуть его вправо, после чего сделать первоначальное левое вращение.
Если поддереву для восстановления баланса требуется поворот вправо, то сначала надо проверить фактор сбалансированности его левого потомка. Если он перевешивает вправо, то прежде повернуть его влево, а после выполнить первоначальное правое вращение.

Рисунок 8 демонстрирует эти правила при решении дилеммы, с которой мы столкнулись на рисунках 6 и 7. Начав с правого поворота вокруг узла С, дерево устанавливается в положение, при котором левый поворот вокруг узла А вернёт его в состояние баланса.

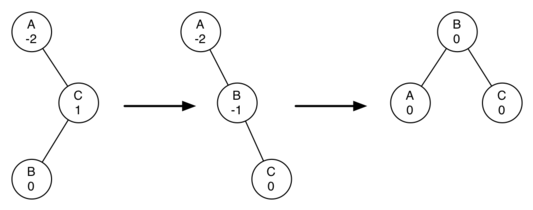
Рисунок 8: Правый поворот с последующим левым вращением

Код, воплощающий эти правила, можно найти в методе rebalance из листинга 3. Правило №1, изложенное выше, реализовано в виде оператора if, начинающегося на строке 2. Правило №2 воплощено в elif, стартующем со строки 8.

Листинг 3

def rebalance(self,node):
  if node.balanceFactor < 0:
   if node.rightChild.balanceFactor > 0:
      self.rotateRight(node.rightChild)
      self.rotateLeft(node)
   else:
      self.rotateLeft(node)
  elif node.balanceFactor > 0:
   if node.leftChild.balanceFactor < 0:
      self.rotateLeft(node.leftChild)
      self.rotateRight(node)
   else:
      self.rotateRight(node)

Вопросы для обсуждения предоставят вам возможность отбалансировать дерево, требующее левого, а затем правого поворота. Дополнительно вы сможете отбалансировать несколько более сложных деревьев, чем представленное на рисунке 8 <fig_rotatelr>.

Постоянно поддерживая баланс дерева, мы будем обеспечивать выполнение метода get за время \(O(log_2(n))\). Но вопрос в том, какова “стоимость” этого метода? Давайте разобьём его на операции, выполняемые put. Поскольку новый узел вставляется, как лист, обновление факторов сбалансированности всех его родителей потребует максимум \(log_2(n)\) операций для каждого уровня дерева. Если обнаруживается, что поддерево разбалансировано, то требуется максимум два поворота, чтобы вернуть его в состояние баланса. Каждое из вращений срабатывает за время \(O(1)\), так что операция put остаётся \(O(log_2(n))\).

К этому моменту у нас есть реализованный функционал АВЛ-дерева, но вы также нуждаетесь в возможности удалить узел. Мы оставляем этот метод с последующими обновлением и балансировкой в качестве упражнения.

Next Section - Заключение по реализациям АТД Map