Матрица смежности¶

Одним из простейших способов реализовать граф является использование двумерной матрицы. В ней каждая строка и столбец представляют собой вершину графа, а хранимое в ячейке на пересечении строки \(v\) и столбца \(w\) значение показывает, что существует ребро из вершины \(v\) к вершине \(w\). Когда две вершины соединены, мы говорим, что они смежные. На рисунке 3 показана матрица смежности для графа с рисунка 2. Значение в ячейке представляет вес ребра между \(v\) и \(w\).

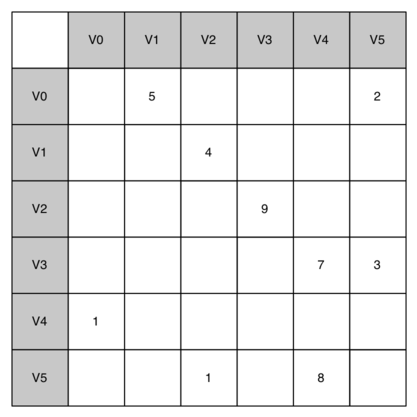
Рисунок 3: Представление графа в виде матрицы смежности.

Преимущество использования матрицы смежности в её простоте. Так же для небольших графов легко увидеть, какие узлы соединены между собой. Однако, обратите внимание, что большинство ячеек в матрице пусты. Про такую матрицу мы говорим, что она “разреженная”. Матрица - не самый эффективный способ хранить разреженные данные. Фактически, в Python вы должны приложить немало усилий, чтобы создать матричную структуру даже наподобие показанной на рисунке 3.

Матрица смежности - хорошее представление графа, который имеет большое количество рёбер. Но что значит “большое”? Сколько рёбер нужно, чтобы заполнить матрицу? Поскольку для каждой вершины графа нужно по одному столбцу и строке, то для заполнения матрицы требуется \(|V|^2\) рёбер. Матрица заполнена, когда каждая вершина соединяется с каждой. В реальном мире существует несколько проблем с таким типом связи между компонентами. Однако, в этой главе все рассматриваемые задачи включают разреженные графы.