Поиск в глубину: общий случай¶
Маршрут коня - особый случай поиска в глубину, целью которого является создание максимально высокого дерева без ветвей. Вообще же обычный поиск в глубину прост. Его задача - искать настолько глубоко, на сколько возможно, соединяя максимальное количество узлов графа с ветвлением только по необходимости.
Весьма вероятно, что при этом получится больше, чем одно дерево. Мы называем их лесом поиска в глубину. Как и в поиске в ширину, здесь используется ссылка на предшественника при создании дерева. Также дополнительно требуются две новых поля в классе Vertex: “время” входа и “время” выхода. Первое будет отслеживать, сколько шагов сделал алгоритм до того, как вершина была впервые обнаружена, а второе - количество шагов алгоритма до того, как вершину окрасили в чёрный цвет. В процессе изучения мы увидим, что оба “времени” обладают весьма любопытными свойствами, которые можно использовать в других алгоритмах.
Код нашего поиска в глубину показан в листинге 5. Поскольку функции dfs и её помощница dfsvisit используют переменную для отслеживания “времени” в процессе вызовов dfsvisit, мы выбрали реализацию кода как методов класса, наследующего классу Graph. Она расширяет класс графа, добавляя атрибут time и два метода dfs и dfsvisit. Если вы посмотрите на строку 11, то заметите, что метод dfs проходит по всем вершинам графа, вызывая dfsvisit на окрашенных в белый цвет. Причина, по которой мы проходим по всем узлам, заключается в том, что требуется выполнить не просто поиск из выбранного стартового узла, но и убедиться, что рассмотрены все вершины графа и ни одна из них не выпала из леса поиска. Оператор for aVertex in self может необычно смотреться, но вспомните: в этом случае self - объект класса DFSGraph. А проход по всем вершинам графа абсолютно естественнен.
Листинг 5
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | from pythonds.graphs import Graph
class DFSGraph(Graph):
def __init__(self):
super().__init__()
self.time = 0
def dfs(self):
for aVertex in self:
aVertex.setColor('white')
aVertex.setPred(-1)
for aVertex in self:
if aVertex.getColor() == 'white':
self.dfsvisit(aVertex)
def dfsvisit(self,startVertex):
startVertex.setColor('gray')
self.time += 1
startVertex.setDiscovery(self.time)
for nextVertex in startVertex.getConnections():
if nextVertex.getColor() == 'white':
nextVertex.setPred(startVertex)
self.dfsvisit(nextVertex)
startVertex.setColor('black')
self.time += 1
startVertex.setFinish(self.time)
|
Хотя нашу реализацию bfs интересовало рассмотрение только тех узлов, через которые существует путь от стартовой точки, возможно создать лес поиска в ширину, который представлял бы кратчайшие пути между всеми парами узлов в графе. Мы оставляем это задание в качестве упражнения. А из следующих двух алгоритмов станет ясно, отчего так важно отслеживать лес поиска в глубину.
Метод dfsvisit начинает работу с единичной вершины startVertex и исследует всех её соседей, окрашенных в белый, настолько глубоко, насколько это возможно. Если вы внимательно посмотрите на код dfsvisit и сравните его с поиском в ширину, то заметите, что эти два алгоритма во многом похожи, за исключением последней строки вложенного цикла for. В ней dfsvisit вызывает сама себя, чтобы продолжить поиск на более глубоком уровне, в то время как bfs добавляет узел в очередь для дальнейшего исследования. Интересно заметить, что там где bfs использует очередь, dfsvisit пользуется стеком. Вы не видите его в коде, но он неявно присутствует в рекурсивном вызове dfsvisit.
Следующая последовательность рисунков иллюстрирует работу алгоритма поиска в глубину для небольшого графа. Пунктирные линии обозначают уже проверенные рёбра, один из узлов которых уже добавлен в дерево поиска. В коде этот тестируется проверкой, что цвет другого узла - не белый.
Поиск начинается с вершины А (рисунок 14). Поскольку все узлы в начале поиска окрашены в белый, алгоритм в неё заходит. Первый шаг при посещении узла - окрасить его в серый (вершина была исследована) и установить “время” входа равным единице. Поскольку А имеет две смежные вершины (B, D), то каждую из них тоже требуется посетить. Мы принимаем произвольное решение заходить в узлы в алфавитном порядке.
Следующей посещаем вершину B (рисунок 15). Её цвет устанавливается серым, а “время” входа равным 2. Этот узел также имеет два смежных (C, D), поэтому далее мы посещаем узел С - в соответствии с алфавитом.
Визит в C (рисунок 16) приводит нас к концу ветки дерева. После окрашивания её в серый и присвоения “времени” входа 3, алгоритм находит отсутствие у С смежных вершин. Это означает, что мы завершили её исследование, так что можно окрасить С в чёрный и задать ей “время” выхода равным 4. Состояние поиска на данный момент вы можете видеть на рисунке 17.
Поскольку С является концом первой ветви, мы возвращаемся в вершину B и продолжаем исследовать смежные с ней узлы. Единственная дополнительная вершина для исследования из В - это D, так что мы посещаем её (рисунок 18) и продолжаем поиск. Эта вершина быстро приводит нас в E (рисунок 19), который имеет два смежных - B и F. Обычно мы исследовали их в алфавитном порядке, но сейчас В уже окрашен в серый цвет. Алгоритм распознаёт, что ему не следует туда заходить, чтобы не загнать себя в цикл, поэтому исследование продолжается для следующей вершины из списка - F (рисунок 20).
F имеет единственный смежный узел - С. Но поскольку он уже окрашен в чёрный, то больше исследовать нечего, и алгоритм достигает конца другой ветви. Отсюда вы можете видеть на рисунках с 21-го по 25-й, как алгоритм возвращается обратно к первому узлу, устанавливает ему “время” выхода и окрашивает его в чёрный.
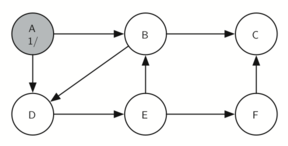
Рисунок 14: Создание дерева поиска в глубину - 10
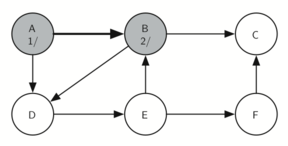
Рисунок 15: Создание дерева поиска в глубину - 11
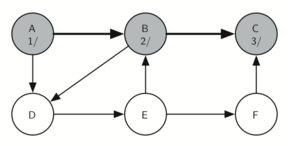
Рисунок 16: Создание дерева поиска в глубину - 12
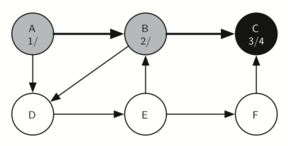
Рисунок 17: Создание дерева поиска в глубину - 13
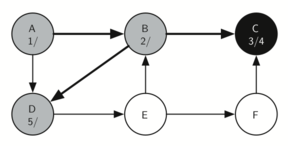
Рисунок 18: Создание дерева поиска в глубину - 14
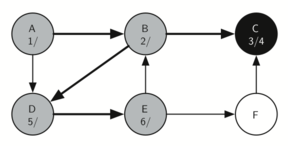
Рисунок 19: Создание дерева поиска в глубину - 15
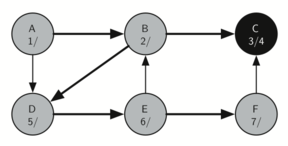
Рисунок 20: Создание дерева поиска в глубину - 16
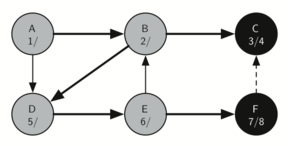
Рисунок 21: Создание дерева поиска в глубину - 17
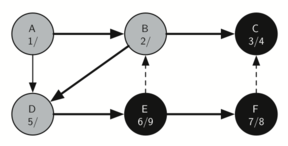
Рисунок 22: Создание дерева поиска в глубину - 18
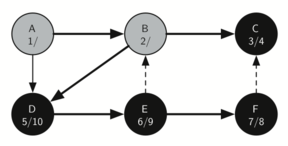
Рисунок 23: Создание дерева поиска в глубину - 19
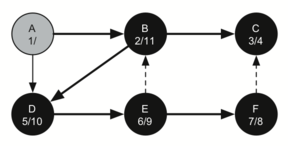
Рисунок 24: Создание дерева поиска в глубину - 20
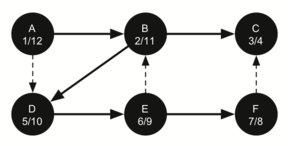
Рисунок 25: Создание дерева поиска в глубину - 21
“Времена” входа и выхода для каждого узла показывают так называемое свойство скобок. Оно означает, что все потомки данного узла в дереве поиска имеют более позднее “время” входа и раннее “время” выхода, чем их предки. Рисунок 26 демонстрирует дерево, сконструированное алгоритмом поиска в глубину.
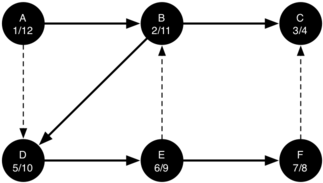
Рисунок 26: Результирующее дерево поиска в глубину