Анализ задачи о ходе коня¶

Это последняя тема, посвящённая задаче о ходе коня; далее мы перейдём к общей версии поиска в глубину. Здесь же поговорим о производительности. В частности, knightTour очень чувствителен к способу, которым вы выбираете следующую вершину для посещения. Например, для доски пять на пять на достаточно быстром компьютере можно проложить путь за время около 1,5 секунд. Но что произойдёт, если взять доску восемь на восемь? В этом случае (в зависимости от скорости компьютера) вы можете до получаса прождать получение результата! Причина этого в том, что наша реализация задачи - экспоненциальный алгоритм размером \(O(k^N)\), где N - число клеток на доске, а k - какая-то малая константа. Рисунок 12 поможет визуализировать причину, по которой так происходит. Корень дерева представляет начальную точку поиска. Из неё алгоритм генерирует и проверяет каждый из возможных ходов, которые может сделать конь. Как мы заметили ранее, число их может зависеть от позиции фигуры на доске. В углах у неё есть только два возможных хода, в клетках, смежных с угловыми, - три, а в середине доски - восемь. Количество возможных ходов для каждой позиции на доске показано на рисунке 13. На следующем уровне дерева из исследуемого положения вновь существует от двух до восьми возможных ходов. Число позиций для исследования связано с количеством узлов в дереве поиска.

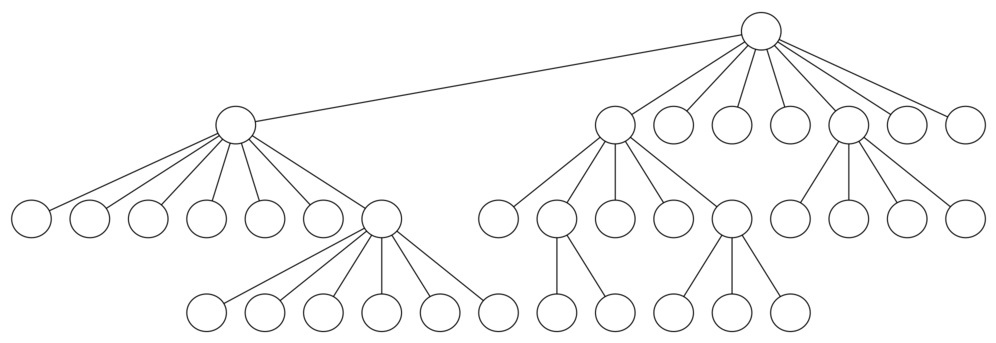
Рисунок 12: Дерево поиска для задачи о ходе коня

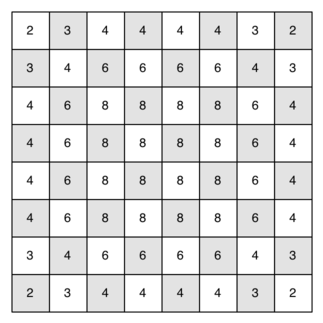
Рисунок 13: Количество возможных ходов для каждой клетки

Мы уже видели, что количество узлов в двоичном дереве высотой N равно \(2^{N+1}-1\). Для дерева, чьи вершины могут иметь до восьми потомков вместо двух, число узлов намного больше. Поскольку фактор ветвления - переменная для каждого узла, количество последних можно оценить, используя среднее значение фактора. Важно отметить, что этот алгоритм экспоненциальный: \(k^{N+1}-1\), где \(k\) - средний фактор ветвления для доски. Давайте посмотрим, насколько быстро он растёт. Для доски 5х5 дерево будет в 25 уровней глубиной или N = 24, если считать первый уровень нулевым. Средний фактор ветвления равен \(k = 3.8\). Таким образом, количество узлов в дереве поиска равно \(3.8^{25}-1\) или \(3.12 \times 10^{14}\). Для доски 6х6 \(k = 4.4\), число узлов - \(1.5\times 10^{23}\). Для обычной же доски 8х8 \(k = 5.25\), а количество узлов \(1.3 \times 10^{46}\). Конечно, поскольку существует несколько решений задачи, мы не будем исследовать каждый конкретный узел, но дробная часть выражения для количества узлов, которые нам необходимо изучить, - всего лишь постоянный множитель, что не меняет экспоненциальный характер проблемы. Мы оставляем вам в качестве упражнения попытку выразить \(k\) в виде функции от размера доски.

К счастью, есть способ ускорить случай 8х8, чтобы он работал примерно одну секунду. В приведённом ниже листинге можно найти код, ускоряющий knightTour. Эта функция (см. листинг 4) называется orderbyAvail и будет использоваться вместо вызова u.getConnections из кода выше. Решающая строка в orderByAvail - десятая. Она гарантирует, что выбранная для дальнейшего продвижения вершина имеет наименьшее количество доступных ходов. Вы можете подумать, что на самом деле это контрпродуктивно: почему бы не выбрать узел, из которого можно совершить максимальное количество перемещений? Такой подход легко опробовать, запустив программу и вставив строку resList.reverse() сразу после сортировки.

Проблема с использованием вершины с наибольшим числом доступных ходов в качестве следующей на пути состоит в том, что конь будет пытаться пройти срединные клетки в самом начале. Когда так происходит, фигура может легко попасть в тупик у одной стороны доски, откуда не будет иметь возможность дойти до непосещённых клеток на другом её краю. С другой стороны, посещение клетки с наименьшим количеством возможных ходов подталкивает фигуру к первоочередному обходу клеток вдоль края доски. Это гарантирует, что конь посетит труднодостижимые углы раньше и сможет использовать средние клетки только при необходимости перепрыгнуть на другую сторону. Применение информации такого рода для ускорения алгоритма называется эвристикой. Люди используют эвристики каждый день для помощи в принятии решений, эвристический поиск часто применяется в области искуственного интеллекта. Данная эвристика называется алгоритмом Вансдорфа - по имени Г. Вансдорфа, опубликовавшего эту идею в 1823 году.

Листинг 4

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

def orderByAvail(n):
    resList = []
    for v in n.getConnections():
        if v.getColor() == 'white':
            c = 0
            for w in v.getConnections():
                if w.getColor() == 'white':
                    c = c + 1
            resList.append((c,v))
    resList.sort(key=lambda x: x[0])
    return [y[1] for y in resList]