Конвертирование целого числа в строку по любому основанию¶

Предположим, вы хотите преобразовать целое число в строку по какому-либо основанию между двойкой и шестнадцатью. Например, перевести число 10 в строковое десятичное "10" или двоичное "1010" представление. Хотя существует множество алгоритмов для решения этой задачи (в том числе тот, что обсуждался в разделе о стеках), рекурсивная формулировка задания будет самой элегантной из них.

Давайте рассмотрим конкретный пример, используя основание 10 и число 769. Предположим, у нас есть последовательность символов, соответствующих первым десяти цифрам, - что-то вроде convString = "0123456789". Тогда конвертировать число, меньшее десяти, в его строковый эквивалент очень просто: достаточно всего лишь найти его в этом перечне. Например, для числа 9 строка будет convString[9] или "9". Если мы сможем организовать разбиение числа 769 на три цифры 7, 6 и 9, то конвертировать их будет просто. Вариант с числом меньше 10 очень подходит для базового случая рекурсии.

Зная наше основание, можно положить, что алгоритм в целом будет включать три компонента:

1. Разбить первоначальное число на последовательность из цифр.
2. Конвертировать каждое из них в строку с помощью поиска.
3. Слить получившиеся односимвольные строки в одну, которая и будет конечным результатом.

Следующий шаг - это придумать, как изменять состояние и продвигаться в строну базового случая. Поскольку мы работаем с числовыми значениями, то давайте рассмотрим, какие математические операции могут уменьшить число. Наиболее очевидными кандидатами будут деление и вычитание. Хотя последнее может работать, не совсем понятно, что из чего требуется вычитать. А вот деление нацело с получением остатка даёт нам чёткое направление. Давайте посмотрим, что произойдёт, если мы разделим число на основание, по которому пытаемся конвертировать.

Разделив 769 на 10 нацело, получим 76 и 9 в остатке. Это даст нам два хороших результата. Во-первых, остаток меньше нашего основания, следовательно, сразу же может быть преобразован в строку. Во-вторых, у нас есть число, меньшее первоначального и приближающееся к базовому случаю. Теперь нужно перевести в строковое представление 76. Вновь использовав деление нацело, получим 7 и 6 в остатке. Наконец, задача свелась к конвертированию 7, что легко может быть сделано, поскольку удовлетворяет условию \(n < base\) базового случая (\(base = 10\)). Последовательность проделанных нами операций проиллюстрирована на рисунке 3. Заметьте, что число, которое мы хотим запомнить, находится в коробочке остатка вдоль правого края диаграммы.

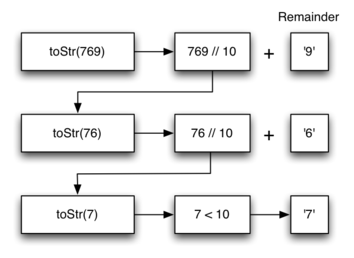
Рисунок 3: Преобразование целого числа в строку по основанию 10.

ActiveCode 3 демонстрирует код на Python, реализующий описанный выше алгоритм для любого основания между двойкой и шестнадцатью.

Обратите внимание, что в строке 3 мы проверяем базовый случай, в котором n должно быть меньше, чем основание, по которому мы конвертируем. Когда мы определяем базовый случай, то останавливаем рекурсию и просто возвращаем строку из последовательности convertString. Строка 6 удовлетворяет требования второго и третьего законов: делает рекурсивный вызов и уменьшает размер задания с помощью деления.

Давайте пройдём по алгоритму ещё раз. На этот раз мы будем конвертировать число 10 в его строковое представление по основанию 2 (“1010”).

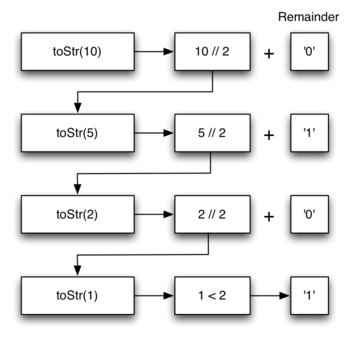
Рисунок 4: Преобразование числа 10 в строку по основанию 2.

Рисунок 4 показывает, что мы получаем искомый результат, вот только цифры находятся в неверном порядке. Алгоритм работает правильно, потому что мы сначала делаем рекурсивный вызов в строке 6, а затем добавляем строковое представление остатка. Если поменять местами возврат из поиска по convertString и возврат из вызова toStr, то результирующая строка будет задом наперёд! Но если придержать операцию слияния до тех пор, пока не вернётся результат рекурсивного вызова, то ответ получит нужный порядок. Это должно напомнить вам обсуждение обратной работы стека в предыдущей главе.