Фрейм стека: реализация рекурсии¶

Предположим, что вместо объединения результатов рекурсивных вызовов toStr со строкой из convertString, мы изменим наш алгоритм таким образом, чтобы он складывал строки в стек перед тем, как сделать рекурсивный вызов. Код такого алгоритма показан в ActiveCode 6.

Каждый раз, когда вызывается toStr, в стек помещается символ. Возвращаясь к предыдущему примеру, мы можем увидеть, что после четвёртого вызова toStr стек будет выглядеть, как показано на рисунке 5. Обратите внимание: теперь мы можем просто вытолкнуть символы из стека и объединить их в итоговый результат "1010".

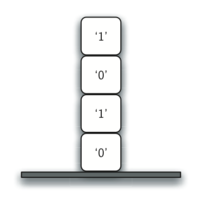
Рисунок 5: Строки, помещённые в стек во время преобразования.

Предыдущий пример даёт нам некоторое представление о том, как в Python реализованы рекурсивные вызовы. При вызове функции для управления её локальными переменными выделяется фрейм стека. Возвращаемое значение к моменту окончания работы функции будет лежать на вершине стека, доступное для вызывающей части программы. Рисунок 6 иллюстрирует стек после оператора return в строке 4.

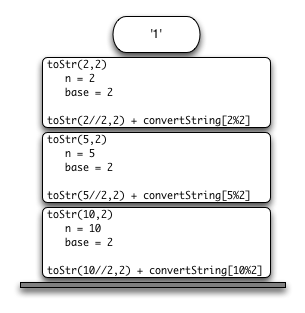
Рисунок 6: Стек вызовов, сгенерированный toStr(10, 2).

Обратите внимание, что вызов toStr(2//2, 2) оставляет возвращаемое значение "1" в стеке. Затем оно подставляется вместо функции toStr(1, 2) в выражение "1" + convertString[2%2], которое оставляет на вершине стека "10". Таким образом, стек вызовов Python работает так же, как и стек, который мы явно использовали в листинге 4. В нашем суммирующем список примере вы можете думать о возвращаемом значении в стеке, как об аккумулирующей переменной.

Также фрейм стека предоставляет область видимости для переменных, используемых функцией. Несмотря на то, что мы вновь и вновь вызываем одну и ту же функцию, каждый вызов создаёт новую область видимости для её локальных переменных.

Если вы хорошо уясните для себя идею стека, то вам будет намного легче писать соответствующие рекурсивные функции.