Хэширование¶
В предыдущих разделах мы смогли усовершенствовать наши алгоритмы поиска, используя преимущества информации о том, где элементы хранятся относительно друг друга. Например, зная, что список упорядочен, мы можем осуществлять поиск за логарифмическое время, используя бинарный алгоритм. В этом разделе мы попытаемся пойти ещё на шаг дальше: построить такую структуру данных, в которой можно будет осуществлять поиск за время \(O(1)\). Эту концепцию называют хэшированием.
Теперь нам надо знать больше, чем просто расположение элемента, когда мы ищем его в коллекции. Если каждый элемент находится там, где ему следует быть, то поиск может использовать только сравнения для обнаружения присутствия искомого. Однако, дальше мы увидим, что это, как правило, не единственный выход.
Хэш-таблица - это коллекция элементов, которые сохраняются таким образом, чтобы позже их было легко найти. Каждая позиция в хэш-таблице (часто называемая слотом) может содержать собственно элемент и целое число, начинающееся с нуля. Например, у нас есть слот 0, слот 1, слот 2 и так далее. Первоначально хэш-таблица не содержит элементов, так что каждый из них пуст. Мы можем сделать реализацию хэш-таблицы, используя список, в котором каждый элемент инициализирован специальным значением Python None. Рисунок 4 демонстрирует хэш-таблицу размером \(m=11\). Другими словами, в ней есть \(m\) слотов, пронумерованных от 0 до 10.

Рисунок 4: Хэш-таблица с 11-ю пустыми слотами
Связь между элементом и слотом, в который он кладётся, называется хэш-функцией. Она принимает любой элемент из коллекции и возвращает целое число из диапазона имён слотов (от 0 до \(m-1\)). Предположим, что у нас есть набор целых чисел 54, 26, 93, 17, 77 и 31. Наша первая хэш-функция, иногда называемая “методом остатков”, просто берёт элемент и делит его на размер таблицы, возвращая остаток в качестве хэш-значения (\(h(item)=item \% 11\)). В таблице 4 представлены все хэш-значения чисел из нашего примера. Обратите внимание: метод остатков (модульная арифметика) обычно присутствует в той или иной форме во всех хэш-функциях, поскольку результат должен лежать в диапазоне имён слотов.
| Элемент | Хэш-значение |
|---|---|
| 54 | 10 |
| 26 | 4 |
| 93 | 5 |
| 17 | 6 |
| 77 | 0 |
| 31 | 9 |
Поскольку хэш-значения могут быть посчитаны, мы можем вставить каждый элемент в хэш-таблицу на определённое место, как это показано на рисунке 5. Обратите внимание, что теперь заняты 6 из 11 слотов. Это называется фактором загрузки и обычно обозначается \(\lambda = \frac {numberofitems}{tablesize}\). В этом примере \(\lambda = \frac {6}{11}\).

Рисунок 5: Хэш-таблица с шестью элементами
Теперь, когда мы хотим найти элемент, мы просто используем хэш-функцию, чтобы вычислить имя слота элемента и затем проверить по таблице его наличие. Эта операция поиска имеет \(O(1)\), поскольку на вычисление хэш-значения требуется константное время, как и на переход по найденному индексу. Если всё находится там, где ему положено, то мы получаем алгоритм поиска за константное время.
Возможно, вы уже заметили, что такая техника работает только если каждый элемент отображается на уникальную позицию в хэш-таблице. Например, если следующим в нашей коллекции будет элемент 44, то он будет иметь хэш-значение 0 (\(44 \% 11 == 0\)). А так как 77 тоже имеет хэш-значение 0, то у нас проблемы. В соответствии с хэш-функцией два или более элементов должны иметь один слот. Это называется коллизией (иногда “столкновением”). Очевидно, что коллизии создают проблемы для техники хэширования. Позднее мы обсудим их в деталях.
Хэш-функции¶
Для заданной коллекции элементов хэш-функция, связывающая каждый из них с уникальным слотом, называется идеальной хэш-функцией. Если мы знаем, что ни один элемент коллекции никогда не изменится, то возможно создать идеальную хэш-функцию (см. упражнения, чтобы узнать об этом больше). К сожалению, для произвольного набора элементов не существует систематического способа сконструировать идеальную хэш-функцию. К счастью, для эффективной работы она нам и не нужна.
Один из способов всегда иметь идеальную хэш-функцию состоит в увеличении размера хэш-таблицы таким образом, чтобы в ней могло быть размещено каждое из возможных значений элементов. Таким образом гарантируется уникальность слотов. Хотя такой подход практичен для малого числа элементов, при возрастании их количества он перестаёт быть осуществимым. Например, для девятизначных индексов социального страхования потребуется порядка миллиарда слотов. Даже если мы захотим всего лишь хранить данные для класса из 25 студентов, то потратим на это чудовищное количество памяти.
Наша цель: создать хэш-функцию, которая минимизировала бы количество коллизий, легко считалась и равномерно распределяла элементы в хэш-таблице. Существует несколько распространённых способов расширить простой метод остатков. Рассмотрим некоторые из них.
Метод свёртки для создания хэш-функций начинает с деления элемента на составляющие одинаковой величины (кроме последнего, который может иметь отличающийся размер). Эти кусочки складываются вместе и дают результирующее хэш-значение. Например, если наш элемент - телефонный номер 436-555-4601, то мы можем взять цифры и рабить их на группы по два (43, 65, 55, 46, 01). После сложения \(43+65+55+46+01\) мы получим 210. Если предположить, что хэш-таблица имеет 11 слотов, то нужно выполнить дополнительный шаг, поделив это число на 11 и взяв остаток. В данном случае \(210\ \%\ 11\) равно 1, так что телефонный номер 436-555-4601 хэшируется в слот 1. Некоторые методы свёртки идут на шаг дальше и перед сложением переворачивают каждый из кусочков разбиения. Для примера выше мы бы получили \(43+56+55+64+01 = 219\), что даёт \(219\ \%\ 11 = 10\).
Другая числовая техника для создания хэш-функций называется методом средних квадратов. Сначала значение элемента возводится в квадрат, а затем из получившихся в результате цифр выделяется некоторая порция. Например, если элемент равен 44, то мы прежде вычислим \(44 ^{2} = 1,936\). Выделив две средние цифры (93) и выполнив шаг получения остатка, мы получим 5 (\(93\ \%\ 11\)). Таблица 5 показывает элементы, к которым применили оба метода: остатков и средних квадратов. Убедитесь, что понимаете, как эти значения были получены.
| Элемент | Остаток | Средний квадрат |
|---|---|---|
| 54 | 10 | 3 |
| 26 | 4 | 7 |
| 93 | 5 | 9 |
| 17 | 6 | 8 |
| 77 | 0 | 4 |
| 31 | 9 | 6 |
Мы также можем создать хэш-функцию для символьных элементов (например, строк). Слово “cat” можно рассматривать, как последовательность кодов его букв.
>>> ord('c')
99
>>> ord('a')
97
>>> ord('t')
116
Затем можно взять эти три кода, сложить их и спользовать метод остатков, чтобы получить хэш-значение (см. рисунок 6). Листинг 1 демонстрирует функцию hash, принимающую строку и размер таблицы и возвращающую хэш-значение из диапазона от 0 до tablesize-1.
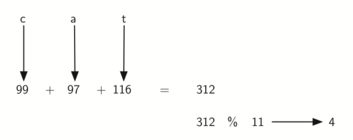
Рисунок 6: Хэширование строки с использованием кодов символов
Листинг 1
def hash(astring, tablesize):
sum = 0
for pos in range(len(astring)):
sum = sum + ord(astring[pos])
return sum%tablesize
Интересное наблюдение: когда мы используем эту хэш-функцию, анаграммы всегда будут иметь одинаковое хэш-значение. Чтобы исправить это, следует использовать позицию символа в качестве веса. Рисунок 7 показывает один из вариантов использования позиционного значения в качестве весового фактора. Модификацию функции hash мы оставляем в качестве упражнения.
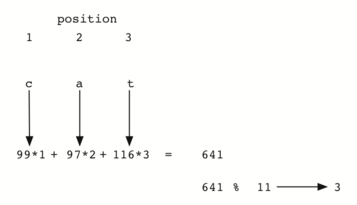
Рисунок 7: Хэширование строки с использованием кодов символов и весов
Вы можете придумать другие числовые способы вычисления хэш-значений для элементов коллекции. Важно только помнить, что эффекитвная хэш-функция не должна являться доминирующей частью процессов хранения и поиска. Если она слишком сложна, то требует много работы на вычисление имени слота. В этом случае проще было бы использовать последовательный или бинарный поиск, описанные выше. Таким образом, сама идея хэширования терпит поражение.
Разрешение коллизий¶
Вернёмся к проблеме коллизий. Когда два элемента хэшируются в один слот, нам требуется систематический метод для размещения в хэш-таблице второго элемента. Этот процесс называется разрешением коллизии. Как мы утверждали ранее, если хэш-функция идеальна, то коллизии никогда не произойдёт. Однако, поскольку часто такое положение дел невозможно, разрешение коллизий становится важной частью хэширования.
Одним из методов разрешения коллизий является просмотр хэш-таблицы и поиск другого свободного слота для размещения в нём элемента, создавшего проблему. Простой способ сделать это - начать с оригинальной позиции хэш-значения и перемещаться по слотам определённым образом до тех пор, пока не будет найден пустой. Заметьте: нам может понадобиться вернуться обратно к первому слоту (циклически), чтобы охватить хэш-таблицу целиком. Этот процесс разрешения коллизий называется открытой адресацией, поскольку пытается найти следующий свободный слот (или адрес) в хэш-таблице. Систематически посещая каждый слот по одному разу, мы действуем в соответствии с техникой открытой адресации, называемой линейным пробированием.
Рисунок 8 показывает расширенный набор целых элементов после применения простой хэш-функции метода остатков (54,26,93,17,77,31,44,55,20). В таблице 4 выше собраны хэш-значения оригинальных элементов, а на рисунке 5 представлено первоначальное содержимое хэш-таблицы. Когда мы пытаемся поместить 44 в слот 0, возникает коллизия. При линейном пробировании мы последовательно - слот за слотом - просматриваем таблицу, до тех пор, пока не найдём открытую позицию. В данном случае это оказался слот 1.
В следующий раз 55, которое должно разместиться в слоте 0, будет положено в слот 2 - следующую незанятую позицию. Последнее значение 20 хэшируется в слот 9. Но поскольку он занят, мы делаем линейное пробирование. Мы посещаем слоты 10, 0, 1, 2 и наконец находим пустой слот на позиции 3.

Рисунок 8: Разрешение коллизий путём линейного пробирования
Поскольку мы построили хэш-таблицу с помощью открытой адресации (или линейного пробирования), важно использовать тот же метод при поиске элемента. Предположим, мы хотим найти число 93. Вчисление его хэш-значения даст 5. Обнаружив в пятом слоте 93, мы вернём True. Но что если мы ищем 20? Теперь хэш-значение равно 9, а слот 9 содержит 31. Нельзя просто вернуть False, поскольку здесь могла быть коллизия. Так что мы вынуждены провести последвательный поиск, начиная с десятой позиции, который закончится, когда найдётся число 20 или пустой слот.
Недостатком линейного пробирования является его склонность к кластеризации: элементы в таблице группируются. Это означает, что если возникает много коллизий с одним хэш-значением, то окружающие его слоты при линейном пробировании будут заполнены. Это начнёт оказывать влияние на вставку других элементов, как мы наблюдали выше при попытке вставить в таблицу число 20. В итоге, кластер значений, хэшируемых в 0, должен быть пропущен, чтобы найти вакантное место. Этот кластер показан на рисунке 9.

Рисунок 9: Кластер элементов для слота 0
Одним из способов иметь дело с кластеризацией является расширение линейного пробирования таким образом, чтобы вместо последовательного поиска следующего свободного места мы пропускали слоты, получая таким образом более равномерное распределение элементов, вызвавших коллизии. Потенциально это уменьшит возникающую кластеризацию. Рисунок 10 показывает элементы после разрешения коллизий с использованием пробирования “плюс 3”. Это означает, что при возникновении коллизии, мы рассматриваем каждый третий слот до тех пор, пока не найдём пустой.

Рисунок 10: Разрешение коллизий с использованием методики “плюс 3”
Общее название для такого процесса поиска другого слота после коллизии - повторное хэширование. С помощью простого линейного пробирования повторная хэш-функция выглядит как \(newhashvalue = rehash(oldhashvalue)\), где \(rehash(pos) = (pos + 1) \% sizeoftable\). Повторное хэширование “плюс 3” может быть определёно как \(rehash(pos) = (pos+3) \% sizeoftable\). В общем случае: \(rehash(pos) = (pos + skip) \% sizeoftable\). Важно отметить, что величина “пропуска” должна быть такой, чтобы в конце концов пройти по всем слотам. В противном случае часть таблицы окажется неиспользованной. Для обеспечения этого условия часто предполагается, что размер таблицы является простым числом. Вот почему в примере мы использовали 11.
Ещё одним вариантом линейного пробирования является квадратичное пробирование. Вместо использования константного значения “пропуска”, мы используем повторную хэш-функцию, которая инкрементирует хэш-значение на 1, 3, 5, 7, 9 и так далее. Это означает, что если первое хэш-значение равно \(h\), то последующими будут \(h+1\), \(h+4\), \(h+9\), \(h+16\) и так далее. Другими словами, квадратичное пробирование использует пропуск, состоящий из следующих один за другим полных квадратов. Рисунок 11 демонстрирует значения из нашего примера после использования этой методики.

Рисунок 11: Разрешение коллизий с помощью квадратичного пробирования
Альтернативным методом решения проблемы коллизий является разрешение каждому слоту содержать ссылку на коллекцию (или цепочку) значений. Цепочки позволяют множеству элементов занимать одну и ту же позицию в хэш-таблице. Чем больше элементов хэшируются в одно место, тем сложнее найти элемент в коллекции. Рисунок 12 показывает, как элементы добавляются в хэш-таблицу с использованием цепочек для разрешения коллизий.
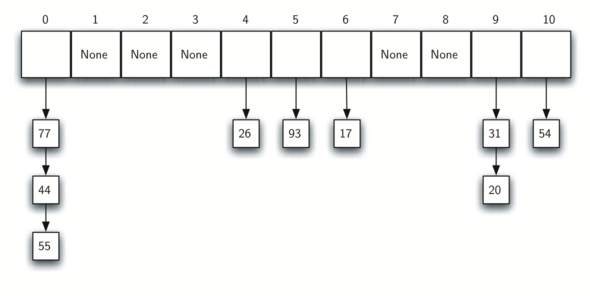
Рисунок 12: Разрешение коллизий с помощью цепочек
Когда мы хотим найти элемент, мы используем хэш-функцию для генерации номера слота, в котором он должен размещаться. Поскольку каждый слот содержит коллекцию, мы используем различные техники поиска, чтобы определить, представлен ли он в ней. Преимуществом данного подхода является вероятность получить гораздо меньше элементов в каждом слоте, так что поиск будет более эффективным. Более подробный анализ мы проведём в конце этой главы.
Самопроверка
Реализация абстрактного типа данных Map¶
Одной из наиболее используемых коллекций Python являются словари. Напомним, что словарь - ассоциативный тип данных, в котором можно хранить пары ключ-значение. Ключи используются для поиска ассоциативных значений данных. Мы часто называем эту идею отображением.
Абстрактный тип данных Map можно определить следующим образом. Его структура - неупорядоченная коллекция ассоциаций между ключами и значениями. Все ключи уникальны, таким образом поддерживаются отношения “один к одному” между ключами и значениями. Операции для такого типа данных представлены ниже:
- Map() Создаёт новый пустой экземпляр типа. Возвращает пустую коллекцию отображений.
- put(key, val) Добавляет новую пару ключ-значение в отображение. Если такой ключ уже имеется, то заменяет старое значение новым.
- get(key) Принимает ключ, возвращает соответствующее ему значение из коллекции или None.
- del Удаляет пару ключ-значение из отображения, используя оператор вида del map[key].
- len() Возвращает количество пар ключ-значение, хранящихся в коллекции.
- in Возвращает True для оператора вида key in map, если данный ключ присутствует в коллекции, или False в противном случае.
Одним из больших преимуществ словарей является то, что, имея ключ, мы можем найти ассоциированное с ним значение очень быстро. Для обеспечения надлежащей скорости требуется реализация, поддерживающая эффективный поиск. Мы можем использовать список с последовательным или бинарным поиском, но правильнее будет воспользоваться хэш-таблицей, описанной выше, поскольку поиск элемента в ней может приближаться к производительности \(O(1)\).
В листинге 2 мы используем два списка, чтобы создать класс HashTable, воплощающий абстрактный тип данных Map. Один список, называемый slots, будет содержать ключи элементов, а параллельный ему список data - значения данных. Когда мы находим ключ, на соответствующей позиции в списке с данными будет находиться связанное с ним значение. Мы будем работать со списком ключей, как с хэш-таблицей, используя идеи, представленные ранее. Обратите внимание, что первоначальный размер хэш-таблицы выбран равным 11. Хотя это число произвольно, важно, чтобы оно было простым. Это сделает алгоритм разрешения коллизий максимально эффективным.
Листинг 2
class HashTable:
def __init__(self):
self.size = 11
self.slots = [None] * self.size
self.data = [None] * self.size
hashfunction реализует простой метод остатков. В качестве техники разрешения коллизий используется линейное пробирование с функцией повторного хэширования “плюс 1”. Функция put (см. листинг 3) предполагает, что в конце-концов найдётся пустой слот, или такой ключ уже присутствует в self.slots. Она вычисляет оригинальное хэш-значение и, если слот не пуст, применяет функцию rehash до тех пор, пока не найдёт свободное место. Если непустой слот уже содержит ключ, старое значение данных будет заменено на новое.
Листинг 3
def put(self,key,data):
hashvalue = self.hashfunction(key,len(self.slots))
if self.slots[hashvalue] == None:
self.slots[hashvalue] = key
self.data[hashvalue] = data
else:
if self.slots[hashvalue] == key:
self.data[hashvalue] = data #replace
else:
nextslot = self.rehash(hashvalue,len(self.slots))
while self.slots[nextslot] != None and \
self.slots[nextslot] != key:
nextslot = self.rehash(nextslot,len(self.slots))
if self.slots[nextslot] == None:
self.slots[nextslot]=key
self.data[nextslot]=data
else:
self.data[nextslot] = data #replace
def hashfunction(self,key,size):
return key%size
def rehash(self,oldhash,size):
return (oldhash+1)%size
Аналогично функция get (см. листинг 4) начинает с вычисления начального хэш-значения. Если искомая величина не содержится в этом слоте, то используется rehash для определения следующей позиции. Обратите внимание: строка 15 гарантирует, что поиск закончится, проверяя, не вернулись ли мы в начальный слот. Если такое происходит, значит все возможные слоты исчерпаны, и элемент в коллекции не представлен.
Кончный метод класса HashTable предоставляет для словарей дополнительный функционал. Мы перегружаем методы __getitem__ и __setitem__, чтобы получать доступ к элементам с помощью []. Это подразумевает, что созданному экземпляру HashTable будет доступен знакомый оператор индекса. Оставшиеся методы мы оставляем в качестве упражнения.
Листинг 4
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 | def get(self,key):
startslot = self.hashfunction(key,len(self.slots))
data = None
stop = False
found = False
position = startslot
while self.slots[position] != None and \
not found and not stop:
if self.slots[position] == key:
found = True
data = self.data[position]
else:
position=self.rehash(position,len(self.slots))
if position == startslot:
stop = True
return data
def __getitem__(self,key):
return self.get(key)
def __setitem__(self,key,data):
self.put(key,data)
|
Следующая сессия демонстрирует класс HashTable в действии. Сначала мы создаём хэш-таблицу и сохраняем в неё несколько элементов с целочисленными ключами и строковыми значениями данных.
>>> H=HashTable()
>>> H[54]="cat"
>>> H[26]="dog"
>>> H[93]="lion"
>>> H[17]="tiger"
>>> H[77]="bird"
>>> H[31]="cow"
>>> H[44]="goat"
>>> H[55]="pig"
>>> H[20]="chicken"
>>> H.slots
[77, 44, 55, 20, 26, 93, 17, None, None, 31, 54]
>>> H.data
['bird', 'goat', 'pig', 'chicken', 'dog', 'lion',
'tiger', None, None, 'cow', 'cat']
Далее мы получаем доступ и изменяем некоторые из элементов в хэш-таблице. Обратите внимание, что значение с ключом 20 заменяется.
>>> H[20]
'chicken'
>>> H[17]
'tiger'
>>> H[20]='duck'
>>> H[20]
'duck'
>>> H.data
['bird', 'goat', 'pig', 'duck', 'dog', 'lion',
'tiger', None, None, 'cow', 'cat']
>> print(H[99])
None
Целиком пример хэш-таблицы можно увидеть в ActiveCode 1.
Пример хэш-таблицы целиком (hashtablecomplete)
Анализ хэширования¶
Как мы заключили выше, в лучшем случае хэширование предоставляет технику поиска за константное время: \(O(1)\). Однако, из-за некоторого числа коллизий с количеством сравнений всё не так просто. Несмотря на то, что полный анализ хэширования выходит за рамки этого текста, мы можем определить несколько общеизвестных результатов, аппроксимирующих количество сравнений, необходимое для поиска элемента.
Наиболее важной частью информации, которую нам надо проанализировать при использовании хэш-таблицы, является фактор загрузки \(\lambda\). Концептуально, если \(\lambda\) мало, то вероятность столкновений низкая. Т.е. элементы вероятнее всего будут находиться в слотах, соответствующих их хэш-значениям. Если же \(\lambda\) велико, то это означает близость таблицы к заполнению, т.е. будет возникать всё больше и больше коллизий. Следовательно, их разрешение будет более сложным, требовать больше сравнений для поиска свободного слота. В случае цепочек увеличение коллизий означает возрастание количества элементов в каждой из них.
Как и раньше, мы будем рассматривать результаты удачного и неудачного поиска. В первом случае, при использовании открытой адресации с линейным пробированием среднее число сравнений приблизительно равно \(\frac{1}{2}\left(1+\frac{1}{1-\lambda}\right)\). Во втором - \(\frac{1}{2}\left(1+\left(\frac{1}{1-\lambda}\right)^2\right)\). Если мы используем цепочки, то среднее количество сравнений будет \(1 + \frac {\lambda}{2}\) для удачного поиска и \(\lambda\) для неудачного.