Бинарный поиск¶
Существует возможность максимально использовать преимущества упорядоченного списка, если делать сравнения с умом. В последовательном поиске, когда мы сравниваем первый элемент, может быть до \(n-1\) элемента, которые нужно ещё просмотреть, если первый - не то, что мы ищем. Вместо того, чтобы искать в списке по порядку, бинарный поиск начинает проверять элементы с находящегося в середине. Если это то, что нам нужно, - всё готово. Если нет, то можно использовать упорядоченную природу списка, исключив половину оставшихся элементов. Когда искомое больше, чем находящийся по середине элемент, то из дальнейшего рассмотрения можно смело исключить “нижнюю” часть, содержащую меньшие величины. Искомое значение (если оно есть в списке) будет находиться в “верхней” части.
Это рассуждение можно повторить для оставшейся половины. Начнём со среднего элемента и сравним его с искомым. Вновь, мы либо обнаружим его, либо разобьём список пополам, вычеркнув половину пространства для поиска. Рисунок 3 показывает, как этот алгоритм быстро находит значение 54. Полностью функция показана в CodeLens 3.
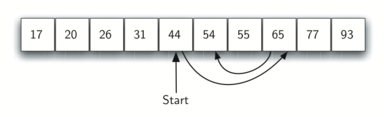
Рисунок 3: Бинарный поиск в упорядоченном списке целых чисел
Бинарный поиск в упорядоченном списке (search3)
Перед тем, как перейти к анализу, отметим, что этот алгоритм - прекрасный пример стратегии “разделяй и властвуй”. “Разделяй и властвуй” означает, что задача делится на маленькие участки, решаемые каким-то образом, а затем ответы компонуются в итоговый результат. Когда мы делаем бинарный поиск в списке, то в начале проверяем серединный элемент. Если искомое меньше его, то можно просто выполнить бинарный поиск для левой части оригинального списка. Аналогично, если искомое больше, то мы проводим бинарный поиск для правой половины. В обоих случаях присутствует рекурсивный вызов функции бинарного поиска на меньшем списке. CodeLens 4 демонстрирует эту рекурсивную версию.
Бинарный поиск - рекурсивный вариант (search4)
Анализ бинарного поиска¶
Для анализа алгоритма бинарного поиска, нам необходимо вспомнить, что каждое сравнение исключает из рассмотрения около половины оставшихся элементов. Каково максимальное число сравнений, которые потребует алгоритм для проверки списка целиком? Если мы начинаем с \(n\) элементов, то после первого сравнения отбросится около \(\frac{n}{2}\) элементов. После второго - порядка \(\frac{n}{4}\). Потом \(\frac{n}{8}\), \(\frac{n}{16}\) и так далее. Сколько раз мы будем разделять список? Таблица 3 поможет найти ответ.
| Сравнения | Приблизительное количество отброшенных элементов |
|---|---|
| 1 | \(\frac {n}{2}\) |
| 2 | \(\frac {n}{4}\) |
| 3 | \(\frac {n}{8}\) |
| ... | |
| i | \(\frac {n}{2^i}\) |
Процесс разбиения закончится на списке, содержащем всего один элемент. Им может оказаться или не оказаться то, что мы ищем. В любом случае, дело сделано. Количество сравнений, необходимых до попадания в эту точку равно \(i\), где \(\frac {n}{2^i} =1\). Решив уравнение для \(i\), получаем \(i=\log n\). Максимальное количество сравнений является логарифмом по отношению к количеству элементов в списке. Таким образом, бинарный поиск будет \(O(\log n)\).
Но нужно разобраться с ещё одним дополнительным вопросом по анализу. В рекурсивном решении, показанном выше, рекурсивный вызов binarySearch(alist[:midpoint],item) использует оператор среза, чтобы создать левую половину списка, которая затем будет передана следующему вызову (аналогично в случае правой половины). Анализ, проделанный выше, предполагает, что эта операция занимает константное время. Однако, мы знаем, что оператор среза в Python вообще-то \(O(k)\). Таким образом, бинарный поиск, использующий срез, не будет выполняться за строго логарифмическое время. К счастью, это можно исправить, передавая кроме списка начальный и конечный индексы его элементов. Индексы могут быть вычислены способом из листинга 3. Реализацию этой идеи мы оставляем в качестве упражнения.
Несмотря на то, что бинарный поиск в целом лучше последовательного, важно отметить, что при малых \(n\) дополнительные расходы на сортировку меньше не становятся. Фактически, мы всегда должны решать, насколько выгодно делать дополнительную работу по сортировке, чтобы воспользоваться преимуществами поиска. Если мы можем отсортировать список единожды, а потом искать в нём много раз, то цена сортировки значения не имеет. Однако, для больших списков даже единичная сортировка может быть настолько затратной, что просто провести последовательный поиск от начала может стать наилучшим решением.
Самопроверка