Последовательный поиск¶
Когда элементы данных хранятся коллекцией в виде списка, мы говорим, что между ними линейные или последовательные отношения. Каждый элемент хранится на определённой позиции относительно прочих. В списках Python она задаётся индексом данного элемента. Поскольку значения индексов упорядочены, мы имеем возможность последовательно проходить по ним. Этот процесс приводит к нашей первой поисковой технике - последовательному поиску.
Рисунок 1 демонстрирует, как работает такой поиск. Начиная с первого элемента в списке, мы просто движемся от значения к значению, следуя внутреннему порядку последовательности, до тех пор, пока либо не найдём то, что ищем, либо не достигнем последнего элемента. Второй случай означает, что последовательность искомое не содержит.
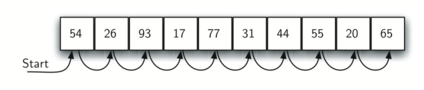
Рисунок 1: Последовательный поиск в списке целых чисел
Реализация этого алгоритма на Python показана в CodeLens 1. Функция требует список и элемент, который мы ищем, а возвращает логическое значение, говорящее о его присутствии. Булева переменная found инициализируется значением False, и если элемент обнаруживаем в списке, то ей присваивается True.
Последовательный поиск в неупорядоченном списке (search1)
Анализ последовательного поиска¶
Для анализа алгоритма поиска нам нужно определиться с базовым блоком вычислений. Напомним, что обычно им является распространённый шаг, который необходимо повторять, чтобы решить задачу. Для поиска имеет смысл подсчитывать количество производимых сравнений. Каждое сравнение может (или не может) обнаружить искомый элемент. В дополнение мы сделаем ещё одно предположение. Список будет неупорядочен, т.е. элементы размещаются в нём случайным образом. Другими словами, вероятность найти искомое на данной позиции одинакова для всех индексов.
Если элемент не в списке, то единственный способ узнать об этом - сравнить его со всеми имеющимися значениями. Если имеется \(n\) элементов, то последовательный поиск потребует \(n\) сравнений, чтобы открыть отсутствие элемента. Если же элемент в списке присутствует, то анализ уже не столь очевиден. Вообще, есть три различных сценария. В лучшем случае мы найдём элемент на первой же позиции, которую рассмотрим, - в самом начале списка. Нам потребуется всего одно сравнение. В худшем случае мы будем искать элемент, пока не дойдём до самого последнего - n-го - сравнения.
Что можно сказать о среднем случае? В нём мы найдём элемент примерно на середине списка. Т.е. нам надо будет сравнить \(\frac{n}{2}\) значения. Однако, напомним, что для больших \(n\) коэффициенты (вне зависимости от их величины) теряют значение при аппроксимации. Так что сложность последовательного поиска равна \(O(n)\). Таблица 1 суммирует результаты этих рассуждений:
| Вариант | Наилучший случай | Наихудший случай | Усреднённый случай |
|---|---|---|---|
| Элемент присутствует | \(1\) | \(n\) | \(\frac{n}{2}\) |
| Элемент отсутствует | \(n\) | \(n\) | \(n\) |
Ранее мы предполагали, что элементы в нашей последовательности размещены произвольно, так что между ними нет относительного упорядочения. Что произойдёт с последовательным поиском, если элементы будут каким-либо образом упорядочены? Сможем ли мы получить возможность для более эффективной методики поиска?
Предположим, список значений был построен таким образом, что они расположены в нём по возрастанию, от наименьшего к наибольшему. Если искомый элемент есть в списке, то вероятность для него быть на любой из \(n\) позиций такая же, как и раньше. Нам по-прежнему необходимо то же количество сравнений для поиска. Однако, для случая, когда элемент в списке отсутствует, у нас есть небольшое преимущество. Рисунок 2 показывает процесс поиска алгоритмом числа 50. Заметьте, что элементы сравниваются последовательно вплоть до 54. В этот момент у нас имеется некая дополнительная информация. Не только то, что 54 - не тот элемент, который мы ищем, но и что элементы за 54-м однозначно не подойдут, поскольку список отсортирован. В этом случае алгоритму нет смысла идти дальше и просматривать всё до конца, чтобы сказать, что искомое не найдено. Он немедленно остановится. CodeLens 2 показывает этот вариант функции последовательного поиска.
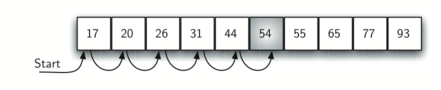
Рисунок 2: Последовательный поиск в упорядоченном списке целых чисел.
Последвательный поиск в упорядоченном списке (search2)
Таблица 2 суммирует эти результаты. Заметьте, в лучшем случае мы обнаружим, что элемент не в списке, просмотрев всего одно значение. В среднем мы будем это знать, просмотрев \(\frac {n}{2}\) элементов. Однако, эта методика по-прежнему имеет \(O(n)\). Резюме: последвательный поиск улучшается при упорядочении списка только для случая, когда искомый элемент в нём отсутствует.
| Элемент присутствует | \(1\) | \(n\) | \(\frac{n}{2}\) |
| Элемент отсутствует | \(1\) | \(n\) | \(\frac{n}{2}\) |
Самопроверка