Дерево синтаксического разбора¶

Закончив с реализацией дерева как структуры данных, рассмотрим примеры его применения при решении некоторых реальных задач. Этот раздел будет посвящён деревьям синтаксического разбора. Они могут использоваться для представления таких конструкций реального мира, как предложения естественного языка или математические выражения.

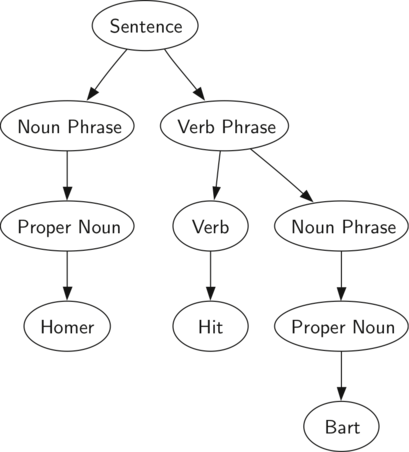
Рисунок 1: Дерево синтаксического разбора простого предложения

На рисунке 1 изображена иерархическая структура простого предложения. Такое представление позволяет нам работать с его отдельными частями, используя поддеревья.

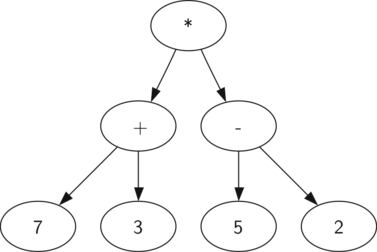
Рисунок 2: Дерево синтаксического разбора выражения \(((7+3)*(5-2))\)

Также в виде дерева синтаксического разбора можно представить математическое выражение наподобие \(((7 + 3) * (5 - 2))\) (см. рисунок 2). Мы уже рассматривали выражения с полной расстановкой скобок: исходя из этого, что можно сказать о данном примере? Нам известно, что умножение имеет более высокий приоритет, чем сложение и вычитание. Однако, благодаря скобкам мы знаем, что здесь сначала нужно вычислить сумму и разность. Иерархия дерева помогает лучше понять порядок вычисления выражения в целом. Перед тем, как найти стоящее на самом верху произведение, требуется произвести сложение и вычитание в поддеревьях. Первая операция - левое поддерево - даст 10, вторая - правое поддерево - 3. Используя свойство иерархической структуры, мы можем просто заменить каждое из поддеревьев на узел, содержащий найденный ответ. Эта процедура даст упрощённое дерево, показанное на рисунке 3.

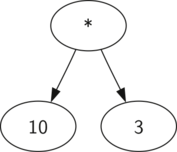
Рисунок 3: Упрощённое дерево синтаксического разбора для \(((7+3)*(5-2))\)

До конца этого раздела мы собираемся как следует протестировать деревья синтаксического разбора. Точнее, будет рассмотрено:

• Как построить дерево разбора для математического выражения с полной расстановкой скобок.
• Как вычислить выражение, хранящееся в дереве разбора.
• Как записать оригинальное математическое выражение из дерева разбора.

Первый шаг при постороении дерева синтаксического разбора - это разбить строку выражения на список токенов. Их насчитывается четыре вида: левая скобка, правая скобка, оператор и операнд. Мы знаем, что прочитанная левая скобка всегда означает начало нового выражения и, следовательно, необходимо создать связанное с ним поддерево. И наоборот, считывание правой скобки сигнализирует о завершении выражения. Так же известно, что операнды будут листьями и потомками своих операторов. Наконец, мы знаем, что каждый оператор имеет обоих своих потомков.

Используя сказанную выше информацию, определим следующие правила:

1. Если считан токен '(' - добавляем новый узел, как левого потомка текущего, и спускаемся к нему вниз.
2. Если считанный один из элементов списка ['+','-','/','*'], то устанавливаем корневое значение текущего узла равным оператору из этого токена. Добавляем новый узел на место правого потомка текущего и спускаемся вниз по правому поддереву.
3. Если считанный токен - число, то устанавливаем корневое значение равным этой величине и возвращаемся к родителю.
4. Если считан токен ')', то перемещаемся к родителю текущего узла.

Перед тем, как писать код на Python, давайте рассмотрим в живую приведённые выше правила. Мы будем работать с выражением \((3 + (4 * 5))\) и разобьём его следующим образом: ['(', '3', '+', '(', '4', '*', '5' ,')',')']. Начинать будем с дерева разбора, содержащего пустой корневой узел. Рисунок 4 демонстрирует его структуру и содержимое по мере вычисления каждого нового токена.

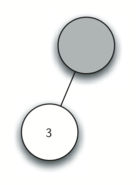
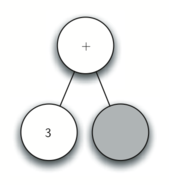
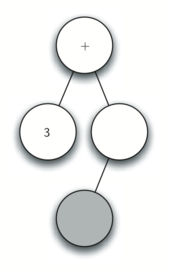
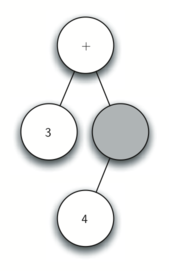
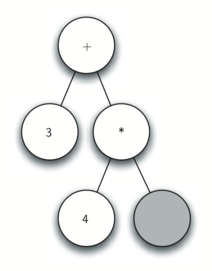
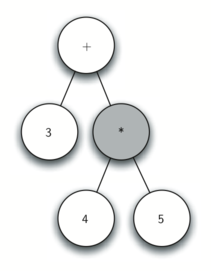
Рисунок 4: Трассировка постороения дерева разбора.

Используя этот рисунок, пройдём по примеру шаг за шагом.

а) Создаём пустое дерево.

б) Читаем ( в качестве первого токена. По правилу 1 создаём новый узел, как левого потомка корня. Делаем его текущим.

в) Считываем следующий токен - 3. По правилу 3 устанавливаем значение текущего узла в 3 и перемещаемся обратно к его родителю.

г) Следующим считываем +. По правилу 2 устанавливаем корневое значение текущего узла в + и добавляем ему правого потомка. Этот новый узел становится текущим.

д) Считываем (. По правилу 1 создаём для текущего узла левого потомка. Этот новый узел становится текущим.

е) Считываем 4. По правилу 3 устанавливаем значение текущего узла равным 4. Делаем текущим родителя 4.

ж) Считываем следующий токен - *. По правилу 2 устанавливаем корневое значение текущего узла равным * и создаём его правого потомка. Он становится текущим.

з) Считываем 5. По правилу 3 устанавливаем корневое значение текущего узла в 5, после чего текущим становится его родитель.

и) Считываем ). По правилу 4 делаем текущим узлом родителя *.

к) Наконец, считываем последний токен - ). По правилу 4 мы должны сделать текущим родителя +. Но такого узла не существует, следовательно, мы закончили.

Из примера выше очевидна необходимость отслеживать не только текущий узел, но и его предка. Интерфейс дерева предоставляет нам способы получить потомков заданного узла - с помощью методов getLeftChild и getRightChild, - но как отследить родителя? Простым решением для этого станет использование стека в процессе прохода по дереву. Перед тем, как спуститься к потомку узла, проследний мы кладём в стек. Когда же надо будет вернуть родителя текущего узла, мы вытолкнем из стека нужный элемент.

Используя описанные выше правила совместно с операциями из Stack и BinaryTree, мы готовы написать на Python функцию для создания дерева синтаксического разбора. Код её представлен в ActiveCode 1.

Четыре правила для постороения дерева разбора закодированы в первых четырёх if-ах 11, 15, 19 и 24 строк ActiveCode 1. В каждом случае вы видите код, воплощающий одно из описанных выше правил с помощью нескольких вызовов методов классов BinaryTree или Stack. Единственная ошибка, на которую в этой функции происходит проверка, - ветка else, вызывающая исключение ValueError, если мы получаем токен, который не можем рапознать.

Итак, дерево синтаксического разбора построено, но что с ним теперь делать? В качестве первого примера, напишем функцию, вычисляющую дерево разбора и возвращающую числовой результат. Для этого будем использовать иерархическу природу дерева. Посмотрите ещё раз на рисунок 2. Напоминаем: оригинальное дерево можно заменять упрощённым, показанным на рисунке 3. Это предполагает возможность написать алгоритм, вычисляющий дерево разбора с помощью рекурсивного вычисления каждого из его поддеревьев.

Как мы уже делали для рекурсивных алгоритмов в прошлом, написание функции начнём с выявления базового случая. Естественным базовым случаем для рекурсивных алгоритмов, работающих с деревьями, является проверка узла на лист. В дереве разбора такими узлами всегда будут операнды. Поскольку объекты, подобные целым или действительным числам, не требуют дальнейшей интерпретации, функция evaluate может просто возвращать значение, сохранённое в листе дерева. Рекурсивный шаг, продвигающий функцию к базовому случаю, будет вызывать evaluate для правого и левого потомков текущего узла. Так мы эффективно спустимся по дереву до его листьев.

Чтобы собрать вместе результаты двух рекурсивных вызовов, мы просто применим к ним сохранённый в родительском узле оператор. В примере на рисунке 3 мы видим, что два потомка корневого узла вычисляются в 10 и 3. Применение к ним оператора умножения даст окончательный результат, равный 30.

Код рекурсивной функции evaluate показан в листинге 1. Сначала мы получаем ссылки на правого и левого потомков текущего узла. Если оба они вычисляются в None, значит этот узел - лист. Это проверяется в строке 7. Если же узел не листовой, то ищем в нём оператор и применяем его к результатам рекурсивных вычислений левого и правого потомков.

Для реализации арифметики мы используем словарь с ключами '+', '-', '*' и '/'. Хранимые в нём значения - функции из модуля операторов Python. Этот модуль предоставляет в наше распоряжение множество часто употребляемых операторов в виде функций. Когда мы ищем в словаре оператор, извлекается связанный с ним объект. А поскольку это функция, то мы можем вызвать её обычным способом function(param1, param2). Таким образом, поиск opers['+'](2,2) эквивалентен operator.add(2,2).

Листинг 1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

def evaluate(parseTree):
    opers = {'+':operator.add, '-':operator.sub, '*':operator.mul, '/':operator.truediv}

    leftC = parseTree.getLeftChild()
    rightC = parseTree.getRightChild()

    if leftC and rightC:
        fn = opers[parseTree.getRootVal()]
        return fn(evaluate(leftC),evaluate(rightC))
    else:
        return parseTree.getRootVal()

Наконец, проследим работу функции evaluate на дереве синтаксического разбора, которое изображено на рисунке 4. В первом вызове evaluate мы передаём ей корень всего дерева в качестве параметра parseTree. Затем получаем ссылки на левого и правого потомков, чтобы убедиться в их существовании. В строке 9 идёт следующий рекурсивный вызов. Мы начинаем с поиска оператора в корне дерева, которым в данном случае является +. Он отображается как вызов функции operator.add, принимающей два параметра. Традиционно для вызова функции первым, что сделает Python, станет вычисление переданных в функцию параметров. В нашем случае оба они - рекурсивные вызовы evaluate. Вычисляя слева направо, сначала выполнится левый рекурсивный вызов, куда передано левое поддерево. Мы обнаружим, что этот узел не имеет потомков, следовательно, является листом. Поэтому хранящееся в нём значение просто вернётся, как результат вычисления. В данном случае это будет целое число 3.

К настоящему моменту у нас есть один параметр, вычисленный для верхнего вызова operator.add. Но мы ещё не закончили. Продолжая вычислять параметры слева направо, сделаем рекурсивный вызов для правого поддерева корня. Обнаружив, что у него есть и правый, и левый потомки, ищем оператор, хранящийся в узле, ('*') и вызываем для него функцию, передавая в неё левого и правого потомков в качестве параметров. В этой точке вычисления оба рекурсивных вызова вернут листья - целые 4 и 5, соответственно. Имея их, вернём результат operator.mul(4,5). Теперь у нас есть все операнды для верхнего оператора +, и остаётся просто вызвать operator.add(3,20). Результат вычисления дерева для выражения \((3 + (4 * 5))\) равен 23.