Узлы и ссылки¶
Наш второй способ представления деревьев будет использовать узлы и ссылки. Для этого случая мы определим класс, чьими атрибутами станут корневое значение и левое и правое поддеревья. Поскольку такое представление ближе к объектно-ориентированной парадигме программирования, то будем развивать его до конца данной главы.
Используя узлы и ссылки, о дереве можно думать, как о структуре, пример которой приведён на рисунке 2.
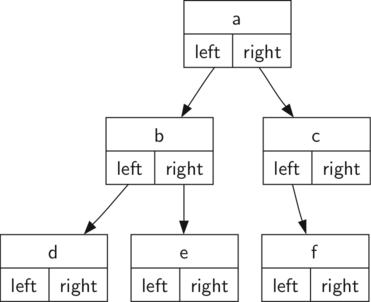
Figure 2: Вариант простого дерева с использованием узлов и ссылок
Начнём с простого определения класса для варианта с узлами и ссылками (листинг 4). Важно помнить, что в этом представлении атрибуты left и right являются ссылками на другие сущности класса BinaryTree. Например, когда мы вставляем нового левого потомка в дерево, мы создаём другой объект BinaryTree и изменяем self.leftChild корня, чтобы этот атрибут ссылался на новое дерево.
Листинг 4
class BinaryTree:
def __init__(self,rootObj):
self.key = rootObj
self.leftChild = None
self.rightChild = None
Обратите внимание, что в листинге 4 конструктор ожидает получить объект некоего вида, чтобы сохранить его в корне. Подобно тому, как вы можете хранить в списке любой объект, коренем дерева может быть любая ссылка. В наших ранних примерах в качестве корневого значения сохранялось имя узла. Используя узлы и ссылки для представления дерева (как это показано на рисунке 2), нам нужно создать шесть сущностей класса ``BinaryTree ``.
Далее давайте рассмотрим функцию, которую требуется написать для строительства дерева за пределы корневого значения. Чтобы добавить левого потомка в дерево, мы создадим новый объект двоичного дерева и поместим в его атрибут корня left ссылку на новый объект. Код для insertLeft показан в листинге 5.
Листинг 5
1 2 3 4 5 6 7 | def insertLeft(self,newNode):
if self.leftChild == None:
self.leftChild = BinaryTree(newNode)
else:
t = BinaryTree(newNode)
t.leftChild = self.leftChild
self.leftChild = t
|
Нам необходимо рассмотреть два случая вставки. Первый - для узла, у которого нет левого потомка. В этом варианте узел просто вставляется в дерево. Второй вариант характеризуется узлом, имеющим левого потомка. Тогда нам надо вставить новый узел и спустить имеющегося потомка на один уровень ниже. Этот случай управляется оператором else в строке 4 листинга 5.
Код для insertRight должен содержать симметричный набор случаев. Здесь также может либо отсутствовать правый потомок, либо существовать необходимость вставить узел между корнем и имеющимся правым потомком. Код операции вставки показан в листинге 6.
Листинг 6
def insertRight(self,newNode):
if self.rightChild == None:
self.rightChild = BinaryTree(newNode)
else:
t = BinaryTree(newNode)
t.rightChild = self.rightChild
self.rightChild = t
Завершая наше определение простого двоичного дерева, напишем методы доступа к корню, правому и левому потомкам (см. листинг 7).
Листинг 7
def getRightChild(self):
return self.rightChild
def getLeftChild(self):
return self.leftChild
def setRootVal(self,obj):
self.key = obj
def getRootVal(self):
return self.key
Теперь у нас есть всё необходимое для создания и манипулирования двоичным деревом. Давайте используем его, чтобы исследовать структуру немного глубже. Создадим простое дерево с узлом a в качестве корня и узлами b и c в качестве потомков. ActiveCode 4 конструирует такое дерево и смотрит, какие значения сохранились в key, left и right. Обратите внимание, что и левый, и правый потомки корня - различные сущности класса BinaryTree. Как мы уже говорили в нашем оригинальном рекурсивном определении дерева, это позволяет нам работать с любым потомком двоичного дерева, как с самим деревом.
Использование реализации с узлами и ссылками (bintree)
Самопроверка
Напишите функцию buildTree, возвращающую дерево, реализованное через узлы и ссылки, которое выглядело бы следующим образом:
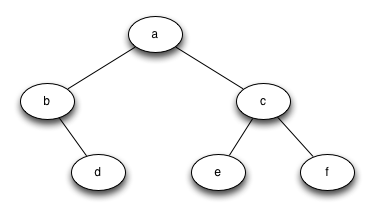
(mctree_3)