Представление дерева в виде списка списков¶

Воплощать дерево в виде списка списков мы начнём со структуры данных Python “список” и напишем для неё функции, определённые выше. Также мы создадим интерфейс - набор операций над списком, немного отличный от тех АТД, которые уже были нами реализованы. Это будет интересно и предоставит в наше распоряжение простую рекурсивную структуру данных, которую потом можно будет изучать и тестировать. В дереве, представленном как список списков, на первой позиции мы будем хранить значение корневого узла. Второй элемент сам по себе будет списком и представит левое поддерево. Третий элемент станет правым поддеревом. Чтобы проиллюстрировать такую технику хранения, рассмотрим пример. Рисунок 1 демонстрирует простое дерево и связанную с ним списковую реализацию.

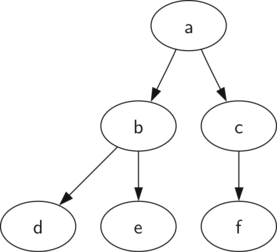
Рисунок 1: Маленькое дерево

myTree = ['a',   #root
      ['b',  #left subtree
       ['d' [], []],
       ['e' [], []] ],
      ['c',  #right subtree
       ['f' [], []],
       [] ]
     ]

Обратите внимание, что у нас есть доступ к каждому из поддеревьев с использованием стандартной списковой индексации. Корень дерева - myTree[0], левое поддерево - myTree[1], правое - myTree[2]. ActiveCode 1 демонстрирует создание простого дерева с использованием списка. После того, как дерево будет готово, мы сможем получить доступ к его корню, правому и левому поддеревьям. Одно из приятных свойств подхода со списком списков заключается в том, что структура списка, представляющего поддерево, твёрдо придерживается определения дерева - она рекурсивна сама по себе! У поддерева есть корень и два пустых списка в качестве листьев. Другое положительное качество списка списков состоит в том, что он легко расширяется до дерева, имеющего много поддеревьев. Т.е. в случае, когда дерево не является двоичным, новое поддерево - это всего лишь новый подсписок.

myTree = ['a', ['b', ['d',[],[]], ['e',[],[]] ], ['c', ['f',[],[]], []] ]
print(myTree)
print('left subtree = ', myTree[1])
print('root = ', myTree[0])
print('right subtree = ', myTree[2])

Использование индексации для доступа к поддеревьям. (tree_list1)

Давайте формализуем это определение с помощью некоторых функций, которые сделают проще использование списков в качестве деревьев. Обратите внимание, мы не собираемся определять новый класс для двоичного дерева. Функции, которые будут написаны, всего лишь помогут манипулировать стандарным списком, с которым мы работаем, как с деревом.

def BinaryTree(r):
    return [r, [], []]

Функция BinaryTree просто создаёт список из корневого узла и двух пустых подсписков в качестве его потомков. Чтобы добавить к корню левое поддерево, нам нужно вставить на вторую позицию новый список. Тут следует быть внимательными. Если на второй позиции уже что-то имеется, то этот факт нужно отследить и сдвинуть элемент вниз по дереву, как левого потомка добавляемого списка.

Листинг 1

def insertLeft(root,newBranch):
    t = root.pop(1)
    if len(t) > 1:
        root.insert(1,[newBranch,t,[]])
    else:
        root.insert(1,[newBranch, [], []])
    return root

Обратите внимание, что прежде, чем вставлять что-либо, мы получаем (возможно пустой) список, связанный с текущим левым потомком. Когда мы вставляем новое левое поддерево, то старое делаем его левым потомком. Благодаря этому мы можем встраивать новый узел на любую позицию в дереве. Код для insertRight аналогичен insertLeft и показан в листинге 2.

Листинг 2

def insertRight(root,newBranch):
    t = root.pop(2)
    if len(t) > 1:
        root.insert(2,[newBranch,[],t])
    else:
        root.insert(2,[newBranch,[],[]])
    return root

Чтобы закончить с набором для создания дерева (см. листинг 3), давайте напишем несколько функций доступа для установки и получения значений в корне и правого и левого поддеревьев.

Листинг 3

def getRootVal(root):
    return root[0]

def setRootVal(root,newVal):
    root[0] = newVal

def getLeftChild(root):
    return root[1]

def getRightChild(root):
    return root[2]

ActiveCode 2 использует только что написанные функции для дерева. Попробуйте поработать с ними самостоятельно. Одно из упражнений попросит вас нарисовать структуру дерева, которое станет результатом такого набора вызовов:

def BinaryTree(r):
    return [r, [], []]

def insertLeft(root,newBranch):
    t = root.pop(1)
    if len(t) > 1:
        root.insert(1,[newBranch,t,[]])
    else:
        root.insert(1,[newBranch, [], []])
    return root

def insertRight(root,newBranch):
    t = root.pop(2)
    if len(t) > 1:
        root.insert(2,[newBranch,[],t])
    else:
        root.insert(2,[newBranch,[],[]])
    return root

def getRootVal(root):
    return root[0]

def setRootVal(root,newVal):
    root[0] = newVal

def getLeftChild(root):
    return root[1]

def getRightChild(root):
    return root[2]

r = BinaryTree(3)
insertLeft(r,4)
insertLeft(r,5)
insertRight(r,6)
insertRight(r,7)
l = getLeftChild(r)
print(l)

setRootVal(l,9)
print(r)
insertLeft(l,11)
print(r)
print(getRightChild(getRightChild(r)))

Сессия Python, демонстрирующая основные функции для работы с деревьями. (bin_tree)

Самопроверка

Q-65: Дан следующий код:

x = BinaryTree('a')
insertLeft(x,'b')
insertRight(x,'c')
insertRight(getRightChild(x),'d')
insertLeft(getRightChild(getRightChild(x)),'e')

Какой из ответов будет правильным представлением дерева?

Напишите функцию buildTree, которая использует функции для списка списков и возвращает дерево, выглядящее примерно так:

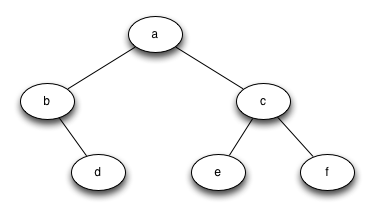
(mctree_2)

Next Section - Узлы и ссылки