Терминология и определения¶

После того, как мы рассмотрели примеры деревьев, дадим формальные определения им и их компонентам.

Узел

Узел - это основная часть дерева. Он может иметь название, которое мы будем называть “ключом”. Также узел может содержать дополнительную информацию, которую мы будем называть “полезной нагрузкой”. Хотя во многих алгоритмах для деревьев ей не уделяется достаточно внимания, для приложений, использующих эту структуру данных, она часто оказывается критичным фактором.

Ветвь

Ветвь - другая фундаментальная часть дерева. Оно соединяет два узла вместе, показывая наличие между ними определённых отношений. Каждый узел (кроме корня) имеет ровно одну входящую ветвь. При этом он может иметь несколько исходящих ветвей.

Корень

Корень дерева - единственный узел, не имеющий входящих ветвей. На рисунке 2 / - корень дерева.

Путь

Путь - это упорядоченный список узлов, соединённых ветвями. Например, Mammal \(\rightarrow\) Carnivora \(\rightarrow\) Felidae \(\rightarrow\) Felis \(\rightarrow\) Domestica - это путь.

Дети (потомки)

Набор узлов \(c\), имеющих входящие ветви от одного узла, называются его детьми. На рисунке 2 узлы log/, spool/ и yp/ - потомки узла var/.

Родитель (предок)

Узел является родителем всех узлов, с которыми связан исходящими ветвями. На рисунке 2 узел var/ является родителем узлов log/, spool/ и yp/.

Братья

Узлы дерева, являющиеся детьми одного родителя, называют братьями. Примером могут послужить etc/ и usr/ в дереве файловой системы.

Поддерево

Поддерево - это набор узлов и ветвей, состоящий родителя и всех его потомков.

Лист

Лист - это узел, у которого нет детей. Например, Human и Chimpanzee - листья на рисунке 1.

Уровень

Уровень узла \(n\) - это число ветвей в пути от корня до \(n\). Например, уровень Felis на рисунке 1 равен пяти. По определению, уровень корня - нулевой.

Высота

Высота дерева равна максимальному уровню любого его узла. Например, высота дерева на рисунке 2 равна двум.

А теперь, определившись с основной терминологией, дадим дереву формальное определение. Фактически, мы дадим две формулировки: первая будет включать узлы и ветви, а вторая (чью полезность мы докажем на практике) будет рекурсивной.

Определение 1: Дерево состоит из набора узлов и набора ветвей, соединяющих пары узлов. Оно имеет следующие свойства:

• Один из узлов дерева определён, как его корень.
• Каждый узел \(n\) (кроме корневого) соединяется ветвью с единственным другим узлом \(p\), где \(p\) - родитель \(n\).
• Каждый узел соединён с корнем единственно возможным путём.
• Если каждый из узлов дерева имеет максимум двух потомков, то такая структура называется двоичным деревом.

На рисунке 3 изображено дерево, удовлетворяющее определению 1. Стрелки на ветвях показывают направление связи.

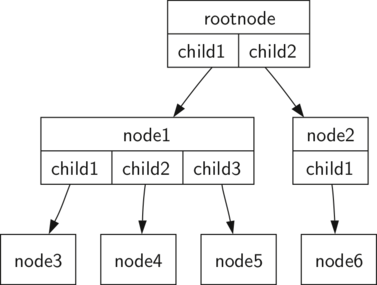
Рисунок 3: Дерево, содержащее набор узлов и ветвей.

Определение 2: Дерево либо пусто, либо содержит корень и нуль или более поддеревьев, каждое из которых тоже является деревом. Корень каждого поддерева соединён ветвью с родительским деревом.

Рисунок 4 иллюстрирует это определение. Используя его, можно сказать, что изображённая структура имеет как минимум четыре узла, поскольку каждый из треугольников, представляющих поддеревья, должен иметь корень. В этом дереве может быть намного больше узлов, но сказать точнее нельзя до тех пор, пока мы не продвинемся по нему глубже.

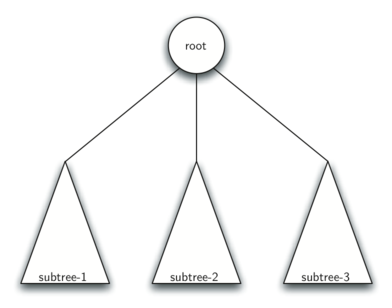
Рисунок 4: Рекурсивное определение дерева