Построение графа для задачи о ходе коня¶

Чтобы представить задачу о ходе коня в виде графа, воспользуемся следующими двумя соображениями: каждая клетка на доске будет узлом, а каждый возможный ход фигуры - ребром. Рисунок 1 иллюстрирует соответствие доступные ходов коня рёбрам графа.

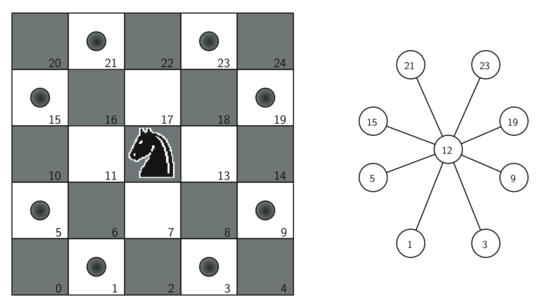
Рисунок 1: Доступные ходы коня, стоящего на клетке 12, и соответствующий им граф

Чтобы построить полный граф для доски \(n \times n\), мы используем код на Python, показанный в листинге 1. Функция knightGraph совершает один проход через всю доску. В каждой из клеток она вызывает вспомогательную функцию genLegalMoves, чтобы создать список возможных ходов для этой позиции. Все они конвертируются в рёбра графа. Другая вспомогательная функция posToNodeId преобразует положение фигуры на доске в терминах столбца и строки в линейный номер вершины, аналогичный номерам, показанным на рисунке 1.

Листинг 1

from pythonds.graphs import Graph

def knightGraph(bdSize):
    ktGraph = Graph()
    for row in range(bdSize):
       for col in range(bdSize):
           nodeId = posToNodeId(row,col,bdSize)
           newPositions = genLegalMoves(row,col,bdSize)
           for e in newPositions:
               nid = posToNodeId(e[0],e[1],bdSize)
               ktGraph.addEdge(nodeId,nid)
    return ktGraph

Функция genLegalMoves (листинг 2) принимает позицию коня на доске и генерирует восемь доступных ходов. Вспомогательная функция legalCoord (листинг 2) проверяет, что данный сгенерированный ход всё ещё лежит на доске.

Листинг 2

def genLegalMoves(x,y,bdSize):
    newMoves = []
    moveOffsets = [(-1,-2),(-1,2),(-2,-1),(-2,1),
                   ( 1,-2),( 1,2),( 2,-1),( 2,1)]
    for i in moveOffsets:
        newX = x + i[0]
        newY = y + i[1]
        if legalCoord(newX,bdSize) and \
                        legalCoord(newY,bdSize):
            newMoves.append((newX,newY))
    return newMoves

def legalCoord(x,bdSize):
    if x >= 0 and x < bdSize:
        return True
    else:
        return False

На рисунке 2 показан полный граф возможных ходов для доски \(8 \times 8\). Это ровно 336 рёбер. Обратите внимание, что вершины, связанные с клетками на краю доски, имеют меньше связей (возможных ходов), чем вершины из середины. Мы снова видим, насколько граф разрежен. Если бы он был полностью связан, то имел бы 4 096 рёбер. Но поскольку в нём их всего лишь 336, то матрица смежности будет заполнена всего на 8.2%

Рисунок 2: Все возможные ходы коня на доске \(8 \times 8\)