Решение задачи о ходе коня¶

Алгоритм, который мы используем для решения задачи о ходе коня, называется поиск в глубину (DFS - от англ. depth first search). В отличие от алгоритма поиска в ширину, обсуждавшегося в предыдущем разделе и строящего один уровень дерева поиска за раз, поиск в глубину создаёт дерево поиска исследуя одну из ветвей настолько глубоко, насколько это возможно. В этом разделе мы рассмотрим два алгоритма для реализации DFS. Первый будет непосредственно решать задачу о ходе коня, явно запрещая посещать исследованный узел более, чем один раз. Второй - более общий случай, позволяющий в процессе конструирования дерева посещать узлы больше одного раза. Он будет использоваться в следующих разделах при разработке дополнительных алгоритмов для графов.

Исследование графа в глубину - в точности то, что нам необходимо для поиска пути ровно в 63 ребра. Мы увидим, что когда алгоритм заходит в тупик (место на графе, откуда больше нет возможных ходов), он возвращается вверх по дереву на следующую по глубине вершину, что позволяет сделать допустимый ход.

Функция knightTour принимает четыре параметра: n - текущую глубину дерева, path - список посещённых вершин, u - вершину, которую мы бы хотели исследовать, и limit - количество узлов в графе. Эта функция рекурсивная. Когда она вызыввается, то прежде всего проверяет базовое условие. Если путь содержит 64 вершины, то мы возвращаем knightTour со статусом True, показывающим, что поиск маршрута успешно завершён. В противном случае исследование продолжается на уровне ниже, для чего выбирается новая вершина и вызвавается knightTour.

DFS тоже использует окрашивание для отслеживания, какие вершины графа были посещены. Непосещённые узлы имеют белый цвет, посещённые - серый. Если все соседи данной вершины уже исследованы, но цель в 64 узла нами не достигнута, то мы зашли в тупик. Следовательно, необходимо вернуться назад. Бэктрекинг происходит в том случае, когда knightTour возвращает False. В поиске в ширину для отслеживания вершины, которую нужно посетить следующей, мы использовали очередь. Поскольку поиск в глубину рекурсивен, для помощи с бэктрекингом неявно используется стек. Когда вызов knightTour возвращает False (строка 11), мы попрежнему находимся внутри цикла while и рассматриваем следующую вершину из nbrList.

Листинг 3

from pythonds.graphs import Graph, Vertex
def knightTour(n,path,u,limit):
        u.setColor('gray')
        path.append(u)
        if n < limit:
            nbrList = list(u.getConnections())
            i = 0
            done = False
            while i < len(nbrList) and not done:
                if nbrList[i].getColor() == 'white':
                    done = knightTour(n+1, path, nbrList[i], limit)
                i = i + 1
            if not done:  # prepare to backtrack
                path.pop()
                u.setColor('white')
        else:
            done = True
        return done

Давайте рассмотрим в действии простой пример работы knightTour. Для отслеживания шагов поиска вы можете обратиться к приведённым ниже рисункам. Будем полагать, что вызов метода getConnections в строке 6 происходит в алфавитном порядке. Начнём с вызова knightTour(0,path,A,6).

knightTour начинает работу с узла А (рисунок 3). А имеет смежные вершины B и D. Поскольку в алфавите B идёт перед D, то DFS выбирает её для дальнейшего исследования, как показано на рисунке 4. Для этого рекурсивно вызывается knightTour. В смежна с C и D, поэтому следующим knightTour выбирает исследование С. Однако, как вы можете видеть из рисунка 5, вершина С - тупик без смежных белых узлов. В этот момент мы меняем цвет С обратно на белый, и вызов knightTour возвращает False. Возврат из рекурсивного вызова эффективно откатывает поиск к вершине В (см. рисунок 6). Следующая вершина в списке исследования - узел D, так что knightTour делает рекурсивный вызов для D (см. рисунок 7). Из неё knightTour может продолжить делать рекурсивные вызовы до тех пор, пока вновь не дойдёт до узла С (см. рисунок 8, рисунок 9 и рисунок 10). Однако в этот раз проверка n < limit даёт отрицательный результат, поэтому мы знаем, что узлы графа закончились. Теперь можно вернуть True, показывая, что маршрут по графу успешно проложен. Когда мы вернём список, path будет иметь значение [A,B,D,E,F,C] - порядок, в котором нужно обойти граф, чтобы посетить каждую вершину всего один раз.

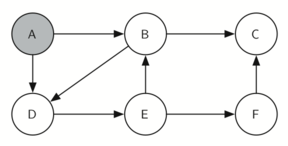
Рисунок 3: Начинаем с узла A

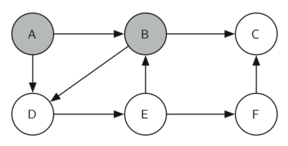
Рисунок 4: Исследуем B

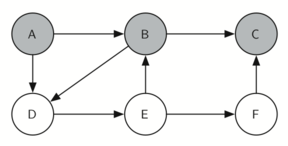
Рисунок 5: Узел C - тупик

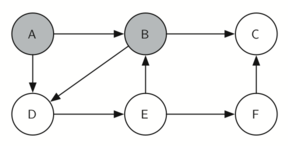
Рисунок 6: Возврат в B

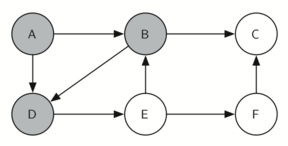
Рисунок 7: Исследуем D

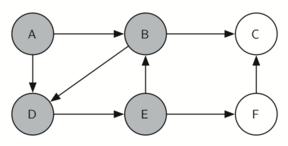
Рисунок 8: Исследуем E

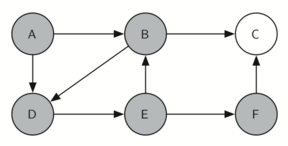
Рисунок 9: Исследуем F

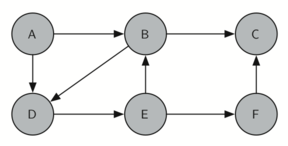
Рисунок 10: Конец

На рисунке 11 показано, как целиком выглядит маршрут по доске 8х8. Таких маршрутов может быть много; некоторые из них будут симметричными. Добавив несколько изменений, вы можете получить замкнутые маршруты, начинающиеся и заканчивающиеся в одной клетке.

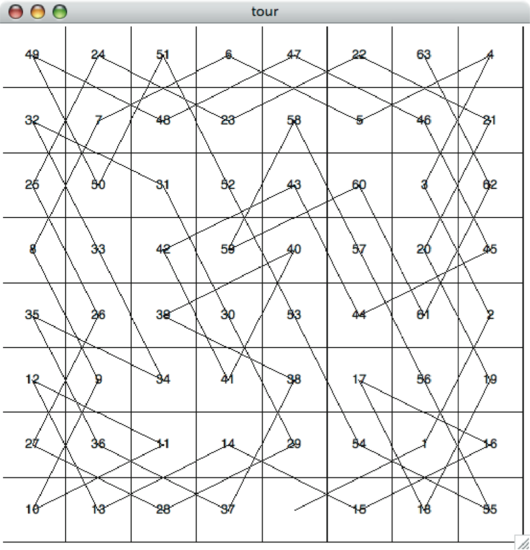
Рисунок 11: Маршрут по доске целиком