Динамическое программирование¶

Многие программы в информатике пишутся для того, чтобы оптимизировать некоторое значение. Например, найти кратчайший путь между двумя точками, найти линию, лучше всего соответствующую набору точек, или найти наименьшее множество объектов, удовлетворяющих некоему критерию. Для их решения существует множество стратегий, которыми пользуются учёные-информатики. Одна из целей этой книги и состоит в том, чтобы представить вам несколько различных способов поиска решения задач. Один из них - динамическое программирование, которое используют при решении задач по оптимизации такого типа.

К классическим примерам задач на оптимизацию является выдача сдачи с использованием наименьшего количества монет. Допустим, вы программист на производстве торговых автоматов. Ваша компания хочет оптимизировать усилия, выдавая как можно меньше монет на сдачу. Предположим, клиент вносит долларовую банкноту и покупает товар за 37 центов. Какое наименьшее количество монет вы можете использовать, чтобы выдать ему сдачу? Ответ: шесть - два четвертака, один десятицентовик и три пенни. Как мы получили ответ в шесть монет? Мы начали с монеты наибольшего номинала в нашем арсенале (четвертак) и использовали их столько, сколько это было возможно. Затем тоже самое проделали со следующейю по номиналу монетой, и так далее. Этот подход называется жадным методом, поскольку пытается решить настолько большой кусок задачи, насколько это возможно здесь и сейчас.

Жадный метод хорошо срабатывает, когда мы используем монеты США, но предположим, что ваша компания решила поставлять свои автоматы в Нижнюю Эльбонию, где в дополнение к монетам номиналом 1, 5, 10 и 25 центов используются монеты в 21 цент. В этом случае жадный метод потерпит поражение в поиске оптимального решения для поиска 63 центов на сдачу. С добавленной 21-центовой монетой он по-прежнему найдёт решение в шесть монет. Однако, правильным ответом будут три монеты по 21-му центу.

Давайте рассмотрим метод, о котором с уверенностью можно сказать, что он всегда найдёт оптимальное решение. Поскольку эта глава о рекурсии, вы можете догаться, что он будет рекурсивным. Начнём с определения базового случая: если мы попытаемся выдать на сдачу некоторую сумму, являющуюся одним из имеющихся номиналов, то ответ прост - одна монета.

Если это невозможно, то у нас есть несколько вариантов. Нам нужен минимум из пенни плюс количество монет, требуемых для первоначальной суммы сдачи минус пенни, или из пятицентовика плюс количество монет для первоначальной суммы сдачи минус пять центов, или из десятицентовика плюс количество монет сдачи с оригинальной суммы минус десять центов, и так далее. Таким образом, необходимое для сдачи количество монет может быть посчитано следующим образом:

Алгоритм, выполняющий то, что мы только что описали, показан в листинге 7. В строке 3 мы проверяем наш базовый случай, т.е. пытаемся дать сдачу одной монетой. Если это не получается, то делаем рекурсивный вызов для каждого номинала, меньшего, чем сумма сдачи. Строка 6 показывает, как отфильтровать список монет, которые меньше текущего значения сдачи, используя генераторы списков. Рекурсивный вызов также уменьшает общую сумму сдачи, которую мы пытаемся выдать, на номинал выбранной монеты. Это происходит в строке 7. Обратите внимание, что там же мы добавляем единицу к количеству монет на счёте, отражая тот факт использования монеты. Просто добавить 1 - это то же самое, что сделать рекурсивный вызов, спрашивающий, не соответствуем ли мы сейчас базовому случаю.

Листинг 7

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

def recMC(coinValueList,change):
   minCoins = change
   if change in coinValueList:
     return 1
   else:
      for i in [c for c in coinValueList if c <= change]:
         numCoins = 1 + recMC(coinValueList,change-i)
         if numCoins < minCoins:
            minCoins = numCoins
   return minCoins

print(recMC([1,5,10,25],63))

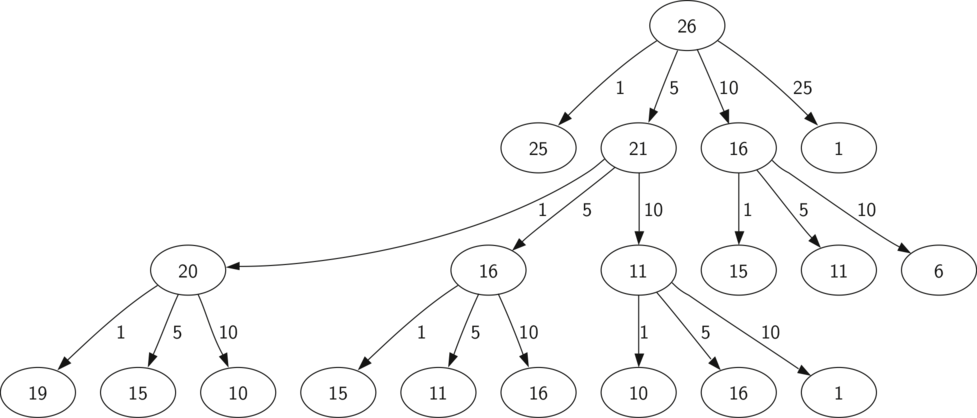
Проблема алгоритма из листинга 7 в том, что он ужасно неэффективный. По факту, для поиска оптимального решения в четыре монеты для 63-х центовой задачи потребуется 67 716 925 рекурсивных вызовов! Чтобы понять фатальный недостаток нашего подхода, посмотрите на рисунок 5, который иллюстрирует небольшую часть 377 вызовов функции, необходимых для поиска оптимального набора монет на сдачу 26-и центов.

Каждый узел графа связан с вызовом recMC. Метка узла показывает сумму сдачи, для которой считается количество монет. Метка стрелки показывает монету, которую мы только что использовали. Следуя графу, мы можем видеть комбинации монет, имеющиеся в любой его точке. Главная проблема в том, что мы повторно делаем слишком много вычислений. Например, граф показывает, что алгоритм будет перевычислять оптимальное количество монет, составляющих сдачу в 15 центов, как минимум трижды. Каждое такое вычисление потребует 52 вызова функции. Очевидно, что мы потратим в пустую много времени и усилий, перевычисляя уже имеющиеся результаты.

Рисунок 3: Дерево вызовов для листинга 7.

Ключ к сокращению объёма работы - это запоминать предыдущие результаты, чтобы избежать перевычисления уже известного. Простым решением будет сохранять результаты с минимальным количеством монет в таблицу. Тогда перед тем, как вычислять новый минимум, мы сначала проверим, не известен ли нам результат заранее. Если он есть в таблице - используем это значение. ActiveCode 3 демонстрирует изменённый алгоритм совместно со схемой поиска в таблице.

Обратите внимание, что в строке 6 мы добавили проверку, не содержится ли в таблице минимальное количество монет для данной суммы сдачи. Если нет, то рекурсивно вычисляем минимум и сохраняем его в таблицу. В этом изменённом алгоритме количество рекурсивных вызовов для 63-х центовой задачи уменьшилось до 221!

Хотя алгоритм из AcitveCode 3 верен, он выглядит несколько рваным. Также если мы посмотрим на список knownResults, то увидим, что в таблице есть несколько дыр. На самом делесделанное нами описывается не термином “динамическое программирование”. Мы улучшили производительность нашей программы с помощью метода, известного как “запоминание” (чаще его называют “кэширование”).

Настоящий алгоритм динамического программирования потребует более систематичного подхода к задаче. Наше решение начинает со сдачи в один цент и систематично работает над получением требуемой суммы. Это гарантирует нам, что на каждом шаге алгоритма мы уже знаем минимальное количество монет, требуемое для сдачи любой меньшей суммы.

Давайте посмотрим, как мы можем заполнить таблицу минимумами монет для сдачи в 11 центов. Рисунок 4 иллюстрирует этот процесс. Мы начинаем с одного цента. Единственное возможное решение - одна монета (пенни). Следующая строка показывает минимум для одного и двух центов. Решение вновь единственное и равняется двум пенни. На пятой строке жизнь становится интереснее. Теперь у нас есть два варианта для рассмотрения: пять пенни или один пятицентовик. Как мы решим, какой из них лучше? Мы проконсультируемся с таблицей и увидим, что сдача в четыре цента даст четыре монеты, плюс ещё одно пенни - итого пять монет. Или мы рассмотрим нуль монет плюс один пятицентовик, что даст нам одну монету. Поскольку минимум из одного и пяти равен одному, то мы сохраняем в таблице единицу. Перенесёмся в конец таблицы и рассмотрим 11 центов. Рисунок 5 показывает три варианта для изучения:

1. Пенни плюс минимальное количество монет для сдачи в 11 - 1 = 10 центов (1)
2. Пятицентовик плюс минимально количество монет для сдачи в 11 - 5 = 6 центов (2)
3. Десятицентовик плюс минимальное количество монет для сдачи в 11 - 10 = 1 цент (1)

Варианты 1 и 3 дают нам ответ в две монеты, что и является минимальным количеством для сдачи в 11 центов.

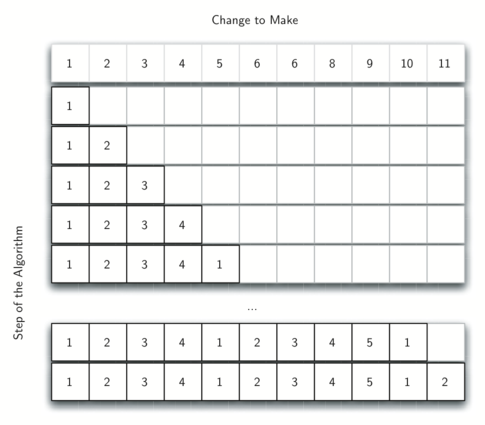
Рисунок 4: Минимальное количество монет, составляющее сдачу.

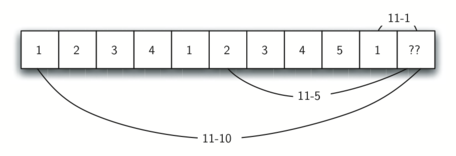
Рисунок 5: Три варианта для нахождения минимального количества монет для сдачи в 11 центов.

Листинг 8 - это алгоритм динамического программирования, решающий нашу задачу о сдаче. dpMakeChange принимает три параметра: список действующих номиналов монет, сумму сдачи, которую мы хотим выдать, и список из минимальных количеств монет, необходимых для выдачи каждого значения. Когда функция закончит свою работу, minCoins будет содержать решение для всех значений от нуля до change.

Листинг 8

def dpMakeChange(coinValueList,change,minCoins):
   for cents in range(change+1):
      coinCount = cents
      for j in [c for c in coinValueList if c <= cents]:
            if minCoins[cents-j] + 1 < coinCount:
               coinCount = minCoins[cents-j]+1
      minCoins[cents] = coinCount
   return minCoins[change]

Обратите внимание, что dpMakeChange не является рекурсивной, хотя начинали мы с рекурсивного решения задачи. Важно понимать, что одна возможность написать рекурсивное решение не означает, что оно будет лучшим или наиболее эффективным. Основная часть работы в этой функции приходится на цикл, который начинается в строке 4. В нём мы рассматриваем все возможные сочетания монет, дающие заданную сумму, определённую cents. Как мы уже делали в примере для одиннадцати центов выше, мы запоминаем минимальные значения и сохраняем их в списке minCoins.

Хотя этот алгоритм выдачи сдачи проделывает хорошую работу по представлению минимального количества монет, он не поможет нам выдать сдачу пока мы не отследим монеты, которые используем. Для этого можно легко расширить dpMakeChange, используя простое запоминание последней добавленной монеты для каждого экземпляра в таблице minCoins. Если мы знаем последнюю добавленную монету, её значение можно просто вычесть, чтобы найти в таблице предыдущий экземпляр, который скажет нам последнюю добавленную монету для составления этой суммы. Мы сможем отслеживат монеты по таблице до тех пор, пока не придём к началу.

ActiveCode 4 демонстрирует алгоритм dpMakeChange, изменённый для возможности отслеживать использованные монеты, вместе с функцией printCoins, проходящей по таблице в обратном направлении и печатающей значение каждой использованной монеты. Это демонстрирует алгоритм, в действии решающий проблему наших друзей из Нижней Эльбонии. Первые две строки в main устанавливают сумму, которую нужно конвертировать, и создают список используемых монет. Следующие две строки инициализируют список, необходимый для хранения результатов. coinsUsed - список монет, использованных для выдачи сдачи, а coinCount - минимальное количество монет для сдачи суммы, связанной с позицией в списке.

Обратите внимание, что монеты, которые мы печатаем, берутся непосредственно из массива coinsUsed. На первом вызове мы начинаем с 63-го индекса в массиве и печатаем 21. Затем берём 63 - 21 = 42 и смотрим на 42-й элемент в списке, где вновь обнаруживаем сохранённое 21. Наконец, 21-й элемент списка тоже содержит 21, что даёт нам три монеты в 21 цент.