Исследование лабиринта¶

В этом разделе мы рассмотрим задачу, имеющую отношение ко всё расширяющемуся миру робототехники: как найти выход из лабиринта? Если у вас есть пылесос Roomba для вашей комнаты в общежитии (или тут не все - студенты колледжа?), то вы можете захотеть перепрограммировать его, используя то, чему научитесь в этом разделе. Задача, которую мы хотим решить, состоит в помощи нашей черепашке найти выход из виртуального лабиринта. Задача лабиринта имеет глубокие корни: греческий миф о Тесее, спустившимся в лабиринт, чтобы убить Минотавра. Тесей использовал клубок нитей, который помог ему вернуться обратно после победы над чудовищем. В нашей задаче мы предположим, что черепашка брошена где-то по середине лабиринта и должна выбраться из него. Посмотрите на рисунок 2, чтобы получить представление о том, чем мы будем заниматься в этом разделе.

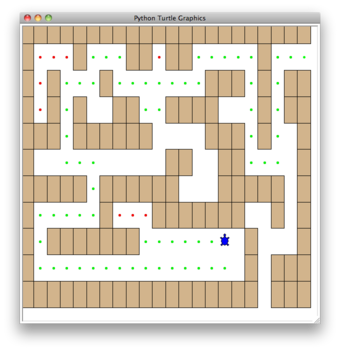
Рисунок 2: Законченная задача поиска пути из лабиринта.

Чтобы сделать нашу жизнь проще, предположим, что лабиринт разбит на “квадраты”. Каждый из них свободен или занят секцией стены. Черепашка может проходить только через свободные квадраты лабиринта. Если она ударяется о стену, то должна попытаться двигаться в другом направлении. Черепашке потребуется систематизированная процедура поиска пути из лабиринта. Например, такая:

• Из начальной позиции пробуем сначала продвинуться на один квадрат на север, а затем рекурсивно повторить процедуру уже отсюда.
• Если попытка из первого шага закончилась неудачей, то делаем шаг на юг и рекурсивно повторяем эту процедуру.
• Если южный путь закрыт, то делаем шаг в западном направлении, после чего опятьрекурсивно применяем процедуру.
• Если шаги на север, юг и запад окончились неудачно, то пробуем идти на восток.
• Если же ни одна из попыток выше не сработала, то выхода из лабиринта нет, и мы потерпели поражение.

Звучит достаточно просто, но есть ещё несколько требующих обсуждения деталей. Предположим, мы делаем первый рекурсивный шаг на север. Согласно нашей процедуре, следующий шаг тоже должен быть в том же направлении. Но если путь заблокирован стеной, мы должны посмотреть на следующий шаг по процедуре и попытаться идти на юг. К несчастью, шаг в этом направлении вернёт нас в первоначальную позицию. Если мы применим рекурсивную процедуру отсюда, мы всего лишь вновь продвинемся на шаг в северном направлении и войдём в бесконечный цикл. Так что нужна стратегия запоминания мест, где мы уже были. В этом случае можно предположить, что у нас есть сумка с хлебными крошками, которые мы разбрасываем по пути. Если мы сделали шаг в данном направлении и обнаружили хлебную крошку в этом квадрате, значит надо незамедлительно вернуться и попытаться идти в следующем направлении по процедуре. Как мы увидим при рассмотрении кода этого алгортма, возвращение - всего лишь возврат из вызова рекурсивной функции.

Поскольку мы работаем с рекурсивными алгоритмами, то давайте рассмотрим базовые случаи. Некоторые из вас уже могли догадаться об их сути, основываясь на предыдущем абзаце. В этом алгоритме четыре базовых случая:

1. Черепашка упирается в стену. Поскольку квадрат занят стеной, то дальнейшее изучение невозможно.
2. Черепашка находится в квадрате, который уже был исследован. Мы не хотим продолжать исследование с этой позиции, иначе зациклимся.
3. Мы нашли внешний край, не занятый стеной. Иными словами, мы вышли из лабиринта.
4. Исследование квадрата закончилось неудачей по всем направлениям.

Для работы программы нужно найти способ представления лабиринта. Чтобы сделать его более интересным, используем модуль turtle для прорисовки и исследования лабиринта. Так можно будет наблюдать алгоритм в действии. Объект “лабиринт”” предоставляет нам следующие методы для написания алгоритма поиска:

• __init__ Считывает данные, представляющие лабиринт, инициализирует его внутреннее представление и находит начальную позицию для черепашки.
• drawMaze Рисует лабиринт на экране.
• updatePosition Обновляет внутреннее представление лабиринта и изменяет позицию черепашки на экране.
• isExit Проверяет, является ли заданная позиция выходом из лабиринта.

Класс Maze также перегружает оператор индекса [], чтобы алгоритм мог легко получить доступ к статусу любого заданного квадрата.

Давайте проверим код функции поиска, которую мы назвали searchFrom. Он показан в листинге 3. Обратите внимание, функция принимает три параметра: объект maze, начальную строку и начальный столбец. Это важно, так как, будучи рекурсивной, функция поиска логически стартует заново на каждом вызове.

Листинг 3

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

def searchFrom(maze, startRow, startColumn):
    maze.updatePosition(startRow, startColumn)
   #  Check for base cases:
   #  1. We have run into an obstacle, return false
   if maze[startRow][startColumn] == OBSTACLE :
        return False
    #  2. We have found a square that has already been explored
    if maze[startRow][startColumn] == TRIED:
        return False
    # 3. Success, an outside edge not occupied by an obstacle
    if maze.isExit(startRow,startColumn):
        maze.updatePosition(startRow, startColumn, PART_OF_PATH)
        return True
    maze.updatePosition(startRow, startColumn, TRIED)

    # Otherwise, use logical short circuiting to try each
    # direction in turn (if needed)
    found = searchFrom(maze, startRow-1, startColumn) or \
            searchFrom(maze, startRow+1, startColumn) or \
            searchFrom(maze, startRow, startColumn-1) or \
            searchFrom(maze, startRow, startColumn+1)
    if found:
        maze.updatePosition(startRow, startColumn, PART_OF_PATH)
    else:
        maze.updatePosition(startRow, startColumn, DEAD_END)
    return found

Проглядывая алгоритм, вы увидите, что первое действие в коде (строка 2) - это вызов updatePosition. Она просто помогает вам визуализировать алгоритм, чтобы можно было наблюдать за тем, как черепашка ищет путь сквозь лабиринт. Затем алгоритм проверяет первые три из четырёх базовых случаев. Упёрлась ли черепашка в стену (строка 5)? Не вернулась ли в уже исследованный квадрат (строка 8)? Не нашла ли выход (строка 11)? Если ни одно из условий не выполнилось, то продолжаем рекурсивный поиск.

Вы можете заметить, что для рекурсивного шага существует четыре рекурсивных вызова searchFrom. Трудно предсказать, сколько из них будет использовано, пока все они не свяжутся оператором or. Если первый вызов searchFrom венёт истину, то ни один из следующих трёх не понадобится. Вы можете интерпретировать это в том смысле, что шаг (row-1, column) (или на север, если удобнее думать географически) лежит на пути, ведущем из лабиринта. Если продвижение на север не приведёт к выходу, то следующий рекурсивный вызов попробует движение на юг. Если южное направление не оправдает себя, то будет испробован путь на запад и, наконец, на восток. Если все четыре рекурсивных вызова вернут ложь, значит мы находимся в тупике. Вам стоит загрузить или набрать программу целиком, чтобы поэкспериментировать над сменой очерёдности этих вызовов.

Код класса Maze показан в листинге 4, листинге 5 и листинге 6. Метод __init__ принимает имя файла как свой единственный параметр. Это текстовый документ, который содержит представление лабиринта с использованием символов “+” для обозначения стен, пробелов для пустых квадратов и буквы “S”, указывающей на начальную позицию. Рисунок 3 - пример того, как может выглядеть файл с данными лабиринта. Внутреннее представление лабиринта - список списков. Каждая строка экземпляра mazelist тоже является списком. Этот второй список содержит по одному символу на квадрат, используя описанные выше договорённости. Для файла данных с рисунка 3 внутреннее представление будет следующим:

[ ['+','+','+','+',...,'+','+','+','+','+','+','+'],
  ['+',' ',' ',' ',...,' ',' ',' ','+',' ',' ',' '],
  ['+',' ','+',' ',...,'+','+',' ','+',' ','+','+'],
  ['+',' ','+',' ',...,' ',' ',' ','+',' ','+','+'],
  ['+','+','+',' ',...,'+','+',' ','+',' ',' ','+'],
  ['+',' ',' ',' ',...,'+','+',' ',' ',' ',' ','+'],
  ['+','+','+','+',...,'+','+','+','+','+',' ','+'],
  ['+',' ',' ',' ',...,'+','+',' ',' ','+',' ','+'],
  ['+',' ','+','+',...,' ',' ','+',' ',' ',' ','+'],
  ['+',' ',' ',' ',...,' ',' ','+',' ','+','+','+'],
  ['+','+','+','+',...,'+','+','+',' ','+','+','+']]

Метод drawMaze использует это внутренне представление, чтобы нарисовать первоначальный вид лабиринта на экране.

Рисунок 3: Пример файла данных для лабиринта.

++++++++++++++++++++++
+   +   ++ ++     +
+ +   +       +++ + ++
+ + +  ++  ++++   + ++
+++ ++++++    +++ +  +
+          ++  ++    +
+++++ ++++++   +++++ +
+     +   +++++++  + +
+ +++++++      S +   +
+                + +++
++++++++++++++++++ +++

Метод updatePosition, показанный в листинге 5, использует аналогичное внутреннее представление для проверки не упёрлась ли черепашка в стену. Он также меняет внутреннее представление, ставя символы ”.” или “-”. Первый используется для обозначения уже посещённых квадратов, второй - если квадрат является частью тупика. Метод updatePosition использует два вспомогательных метода: moveTurtle и dropBreadCrumb, изменяющих изображение на экране.

Наконец, метод isExit использует текущую позицию черепашки для проверки условия выхода. Оно заключается в том, что черепашка подошла к краю лабиринта: нулевым строке или столбцу, крайнему правому столбцу или нижнему ряду.

Листинг 4

class Maze:
    def __init__(self,mazeFileName):
        rowsInMaze = 0
        columnsInMaze = 0
        self.mazelist = []
        mazeFile = open(mazeFileName,'r')
        rowsInMaze = 0
        for line in mazeFile:
            rowList = []
            col = 0
            for ch in line[:-1]:
                rowList.append(ch)
                if ch == 'S':
                    self.startRow = rowsInMaze
                    self.startCol = col
                col = col + 1
            rowsInMaze = rowsInMaze + 1
            self.mazelist.append(rowList)
            columnsInMaze = len(rowList)

        self.rowsInMaze = rowsInMaze
        self.columnsInMaze = columnsInMaze
        self.xTranslate = -columnsInMaze/2
        self.yTranslate = rowsInMaze/2
        self.t = Turtle(shape='turtle')
        setup(width=600,height=600)
        setworldcoordinates(-(columnsInMaze-1)/2-.5,
                            -(rowsInMaze-1)/2-.5,
                            (columnsInMaze-1)/2+.5,
                            (rowsInMaze-1)/2+.5)

Листинг 5

def drawMaze(self):
    for y in range(self.rowsInMaze):
        for x in range(self.columnsInMaze):
            if self.mazelist[y][x] == OBSTACLE:
                self.drawCenteredBox(x+self.xTranslate,
                                     -y+self.yTranslate,
                                     'tan')
    self.t.color('black','blue')

def drawCenteredBox(self,x,y,color):
    tracer(0)
    self.t.up()
    self.t.goto(x-.5,y-.5)
    self.t.color('black',color)
    self.t.setheading(90)
    self.t.down()
    self.t.begin_fill()
    for i in range(4):
        self.t.forward(1)
        self.t.right(90)
    self.t.end_fill()
    update()
    tracer(1)

def moveTurtle(self,x,y):
    self.t.up()
    self.t.setheading(self.t.towards(x+self.xTranslate,
                                     -y+self.yTranslate))
    self.t.goto(x+self.xTranslate,-y+self.yTranslate)

def dropBreadcrumb(self,color):
    self.t.dot(color)

def updatePosition(self,row,col,val=None):
    if val:
        self.mazelist[row][col] = val
    self.moveTurtle(col,row)

    if val == PART_OF_PATH:
        color = 'green'
    elif val == OBSTACLE:
        color = 'red'
    elif val == TRIED:
        color = 'black'
    elif val == DEAD_END:
        color = 'red'
    else:
        color = None

    if color:
        self.dropBreadcrumb(color)

Листинг 6

def isExit(self,row,col):
     return (row == 0 or
             row == self.rowsInMaze-1 or
             col == 0 or
             col == self.columnsInMaze-1 )

def __getitem__(self,idx):
     return self.mazelist[idx]

Целиком программа демонстрируется в ActiveCode 2. Она использует данные из файла maze2.txt, показанного ниже. Отметьте, что это намного более простой пример, потому что выход находится очень близко к стартовой позиции черепашки.

++++++++++++++++++++++
+   +   ++ ++        +
      +     ++++++++++
+ +    ++  ++++ +++ ++
+ +   + + ++    +++  +
+          ++  ++  + +
+++++ + +      ++  + +
+++++ +++  + +  ++   +
+          + + S+ +  +
+++++ +  + + +     + +
++++++++++++++++++++++
  

Измените программу поиска выхода из лабиринта таким образом, чтобы вызовы searchFrom следовали в другом порядке. Посмотрите, как она работает. Можете объяснить, почему её поведение изменилось? Сможете предсказать, по какому пути пойдёт черепаха, следуя изменившейся последовательности вызовов?