Ханойская башня¶

Головоломка о ханойской башне была изобретена французским математиком Эдуардом Лукасом в 1883 году. Его вдохновила легенда, рассказывающая о замке Хинду, где эту загадку задали юным жрецам. В начале времён им дали три стержня и стопку из шестидесяти четырёх золотых дисков, каждый из которых немного меньше предыдущего. Требовалось переставить все диски с одного стержня на другой, соблюдая два строгих условия. Во-первых, за раз можно было перемещать только один диск. Во-вторых, нельзя класть больший диск поверх меньшего. Жрецы работали (и работают по сей день) очень споро, день и ночь, переставляя каждую секунду по одному диску. Легенда гласит, что когда они закончат свою работу, замок обратится в пыль, и мир исчезнет.

Хотя легенда и интересна, вам не стоит беспокоиться о скором конце света. Число ходов, требующихся для правильной перестановки башни из 64 дисков, равняется \(2^{64}-1 = 18,446,744,073,709,551,615\). Со скоростью один ход в секунду это займёт \(584,942,417,355\) лет! Большая цифра для такой несложной на первый взгляд головоломки.

Рисунок 1 показывает пример конфигурации дисков в середине перемещения с первого колышка на третий. Обратите внимание, что (как регламентировано правилами) диски на каждом из колышков складываются таким образом, чтобы меньший всегда лежал на большем. Если вы не пытались раньше решить эту головоломку, то можете попробовать сейчас. Для это не нужны настоящие диски и стержни - сработает и стопка книг или листочков бумаги.

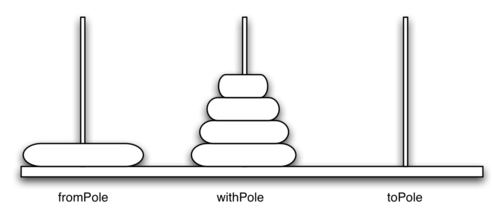
Рисунок 1: Пример расположения дисков ханойских башен.

Как нам решить эту задачу рекурсивно? С чего бы вы начали? Что является здесь базовым случаем? Давайте подумаем над этим от конца к началу. Предположим, изначально на первом колышке у вас находится башня из пяти дисков. Если вы уже знаете, как передвинуть четыре из них на второй колышек, то можете с лёгкостью переложить нижний диск на стержень №3, а затем переложить туда же башню со стержня №2. Но что, если вы понятия не имеете, как переместить башню из четырёх верхних? Предположим, что вы знаете, как передвинуть башню из трёх верхних дисков на третий колышек. Тогда с перемещением четвёртого трудностей не возникнет: переложите его на второй стержень, а затем положите сверху те три, что нанизаны на третий колышек. Но если вы не знаете как переместить три? Что ж, можно переложить башню из двух дисков на стержень №2, а третий - на стержень №3, а потом сверху положить башню из двух. Но если вы до сих пор не понимаете, как это сделать? Уверен, что вы согласитесь: переместить один диск на третий колышек легче лёгкого - тривиальнее вы ничего не найдёте. Звучит как базовый случай, а?

Вот общая схема того, как переместить башню с исходного стержня на заданный с использованием промежуточного:

1. Передвинуть башню из (количество дисков - 1) на промежуточный колышек, используя конечный стержень.
2. Положить оставшийся диск на конечный стержень.
3. Переместить башню из оставшихся на промежуточном стержне дисков на конечный, используя первоначальный колышек.

Пока мы следуем правилу, что больший диск находится внизу стека, мы можем использовать три описанных выше шага рекурсивно, обрабатывая любые большие диски, даже если их там ещё нет. Единственная вещь, которую мы упустили в схеме выше, - это идентификация базового случая. Простейшая задача ханойских башен - это башня из одного диска. В этом случае нам нужно передвинуть единственный диск на его конечное место назначения. Башня из одного диска будет нашим базовым случаем. В дополнение, шаги схемы выше ведут к базовому случаю, уменьшая каждый раз высоту башни на единицу в пунктах 1 и 3. Листинг 1 показывает код на Python для решения задачи ханойских башен.

Листинг 1

1
2
3
4
5

def moveTower(height,fromPole, toPole, withPole):
    if height >= 1:
        moveTower(height-1,fromPole,withPole,toPole)
        moveDisk(fromPole,toPole)
        moveTower(height-1,withPole,toPole,fromPole)

Заметьте, что листинг 1 практически идентичен словесному описанию. Ключ к простоте алгоритма в том, что мы делаем два различных рекурсивных вызова, один в строке 3, а второй - в строке 5. В строке 3 мы перемещаем все диски, кроме нижнего, с начального стержня на промежуточный. Следующая строка просто переставляет нижний диск на его конечную позицию. Затем в строке 5 мы перемещаем башню с промежуточного стержня поверх наибольшего диска. Базовый случай обнаруживается, когда высота башни равна нулю. В этом случае ничего не происходит, поэтому функция moveTower делает пустой возврат. При обработке базового случая важно помнить, что простой возврат из moveTower - это то, что в итоге позволяет функции moveDisk быть вызванной.

Функция moveDisk, показанная в листинге 2, очень проста. Всё, что она делает, - это печатает, что диск был передвинут с одного стержня на другой. Если вы наберёте и запустите программу moveTower, то увидите, как она даст вам очень эффективное решение головоломки.

Листинг 2

def moveDisk(fp,tp):
    print("moving disk from",fp,"to",tp)

Программа в ActiveCode 1 даёт полное решения для задачи с тремя дисками.

Теперь, когда вы можете видеть код и для moveTower, и для moveDisk, то можете задаться вопросом, почему у нас нет структуры данных, которая явно отслеживает, какой диск на каком стержне находится. Вот подсказка: если вы будете явно отслеживать диски, то вам, возможно, придётся использовать три объекта Stack - по одному для каждого стержня. Ответ в том, что Python предоставляет стеки в наше распоряжение неявно, когда нам это нужно.