Сортировка вставками¶
Сортировка вставками, имея по-прежнему \(O(n^{2})\), работает несколько иначе. Она всегда поддерживает в сортированном виде подсписок на нижних индексах списка. Каждый новый элемент “вставляется” в упорядоченный на прошлой итерации подсписок так, чтобы тот остался сортированным и стал на один элемент больше. Рисунок 4 демонстрирует процесс сортировки вставками. Затенённые элементы представляют собой упорядоченные подсписки, которые алгоритм создаёт на каждом проходе.

Начнём с предположения, что список из одного элемента (под номером 0) уже отсортирован. На каждом проходе, для каждого элемента с первого по \(n-1\), текущий элемент сравнивается с уже отсортированными. Поскольку мы просматриваем отсортированный подсписок в обратном порядке, то сдвигаем большие элементы вправо. При обнаружении меньшего элемента или конца подсписка текущий элемент вставляется на соответствующую позцию.
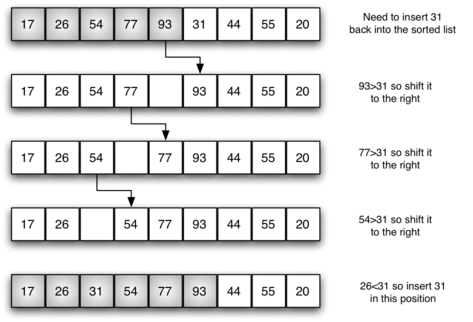
На рисунке 5 детально показан пятый проход. В этой точке алгоритма сортированный список из пяти элементов содержит 17, 26, 54, 77 и 93. Мы хотим вставить в него 31. Первое сравнение с 93 приводит к тому, что 93 сдвигается вправо. Так же сдвигаются 77 и 54. Когда мы наталкиваемся на элемент 26, процесс смещения прекращается, и 31 становится на свободное место. Теперь у нас есть отсортироанный список из шести элементов.
Реализация insertionSort (ActiveCode 4) демонстрирует, что вновь выполняется \(n-1\) проход для сортировки n элементов. Итерации начинаются с индекса 1 и движутся до \(n-1\) позиции, поскольку все эти элементы должны быть вставлены в отсортированный список. В строке 8 происходит операция сдвига, которая перемещает значение на одну позицию вверх по списку, создавая место для вставки. Помните, что полноценный обмен, как в предыдущих алгоритмах, здесь не происходит.
Максимальное количество сравнений для сортировки вставками равно сумме первых \(n-1\) целых. Вновь, это \(O(n^{2})\). Однако, в наилучшем случае на каждом проходе потребуется всего одно сравнение. Это произойдёт, когда список уже отсортирован.
Важное замечание о противопоставлении сдвига и обмена: в общем операция сдвига требует приблизительно трети от вычислительной работы обмена, поскольку делается всего одно присваивание. В контрольных исследованиях сортировка вставками имеет очень хорошую производительность.
Сортировка вставками (lst_insertion)
Для большей детализации, CodeLens 4 позволят вам пошагово пройти весь алгоритм.
Трассировка сортировки вставками (insertionsortcodetrace)