Сортировка Шелла¶

Сортировку Шелла иногда называют “сортировкой с уменьшением инкремента”. Она улучшает сортировку вставками, разбивая первоначальный список на несколько подсписков, каждый из которых сортируется по отдельности. Оригинальный способ выбора таких подсписков - ключевая идея сортировки Шелла. Вместо того, чтобы выделять подсписки из стоящих рядом элементов, сортировка Шелла использует инкремент i (приращение), чтобы создавать подсписки из значений, отстоящих на расстоянии i друг от друга.

Это можно увидеть на рисунке 6. Изображённый на нём список состоит из девяти элементов. Если мы используем тройку в качестве инкремента, то получим три подсписка, каждый из которых можно отсортировать вставками. После завершения этих сортировок мы получим список с рисунка 7. Хотя он ещё не отсортирован до конца, случилось нечто весьма интересное. Сортируя эти подсписки, мы переместили элементы ближе друг к другу относительно того, где они были раньше.

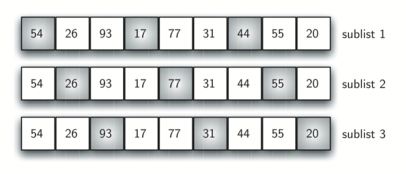
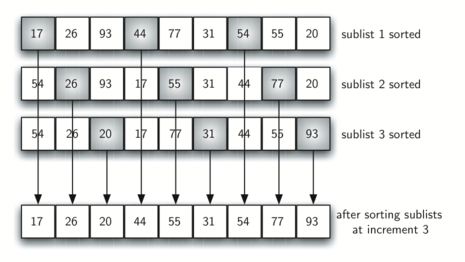
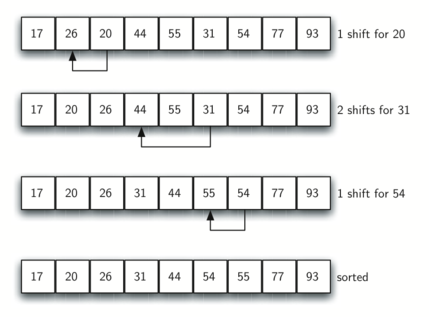
Рисунок 8 демонстрирует окончательную сортировку вставками с использованием приращения 1 - другими словами, стандартную сортировку вставками. Обратите внимание, что, благодаря проведению предварительных сортировок подсписков, сейчас мы сократили общее число операций смещения, необходимых для расположения элементов списка в правильном порядке. В нашем случа требуется всего четыре сдвига, чтобы завершить процесс.

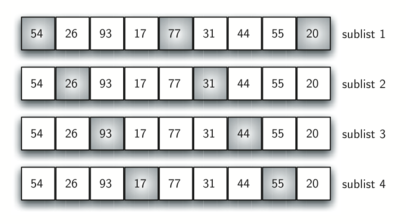
Ранее мы уже говорили, что способ, которым выбирается инкремент, - уникальное свойство сортировки Шелла. Функция, показанная в ActiveCode 5, использует различный набор инкрементов. Мы начинаем с \(\frac {n}{2}\) подсписков. На следующем проходе сортируются \(\frac {n}{4}\) подсписков. Наконец, единственный список сортируется с помощью базовой сортировки вставками. Рисунок 9 показывает первые подсписки из нашего примера, использующие этот инкремент.

Следующий вызов функции shellSort демонстрирует списки, частично отсортированные после каждого приращения, и финальную сортировку с инкрементом 1.

Для большей детализации CodeLens 5 пошагово проведут вас через алгоритм.

На первый взгляд может показаться, что сортировка Шелла не лучше, чем вставками, поскольку она делает полную сортировку вставками на последнем шаге. Однако, получается так, что эта итоговая сортировка не требует большого количества сравнений (или сдвигов), поскольку список уже был частично отсортирован с помощью ранних сортировок вставками (как это описано выше). Другими словами, каждый проход делает список “более сортированным” по отношению к предыдущему. Поэтому финальный проход получается таким эффективным.

Хотя общий анализ сортировки Шелла выходит за пределы рассмотрения для этого текста, мы можем сказать, что он находится между \(O(n)\) и \(O(n^{2})\), в зависимости от поведения, описанного выше. Для инкрементов, показанных в листинге 5, производительность \(O(n^{2})\). Изменив инкремент (например, на \(2^{k}-1\) (1, 3, 7, 15, 31 и так далее)) получим производительность сортировки Шелла \(O(n^{\frac {3}{2}})\).